题目内容
已知两直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m,n的值,使
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2,且l1在y轴上的截距为-1.
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2,且l1在y轴上的截距为-1.
(1)将点P(m,-1)代入两直线方程得:m2-8+n=0 和 2m-m-1=0,
解得 m=1,n=7.
(2)由 l1∥l2 得:m2-8×2=0,m=±4,
又两直线不能重合,所以有 8×(-1)-mn≠0,对应得 n≠2m,
所以当 m=4,n≠-2 或 m=-4,n≠2 时,L1∥l2.
(3)当m=0时直线l1:y=-
和 l2:x=
,此时,l1⊥l2,-
=-1⇒n=8.
当m≠0时此时两直线的斜率之积等于
,显然 l1与l2不垂直,
所以当m=0,n=-8时直线 l1 和 l2垂直,且l1在y轴上的截距为-1.
解得 m=1,n=7.
(2)由 l1∥l2 得:m2-8×2=0,m=±4,
又两直线不能重合,所以有 8×(-1)-mn≠0,对应得 n≠2m,
所以当 m=4,n≠-2 或 m=-4,n≠2 时,L1∥l2.
(3)当m=0时直线l1:y=-
| n |
| 8 |
| 1 |
| 2 |
| n |
| 8 |
当m≠0时此时两直线的斜率之积等于
| 1 |
| 4 |
所以当m=0,n=-8时直线 l1 和 l2垂直,且l1在y轴上的截距为-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
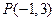 且垂直于直线
且垂直于直线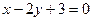 的直线方程为( )
的直线方程为( )