题目内容
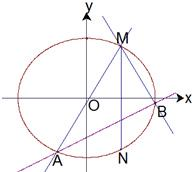 (2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆C:
(2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(I)求椭圆C的方程;
(II)若点N到直线AM,BM距离的和为6
| 2 |
分析:(I)设直线l的方程为y=
x+m(m∈R),代入b2x2+a2y2=a2b2得:(b2+
)x2+ma2x+a2m2-a2b2=0设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R),则x1+x2=-
,x1•x2=
,再由SMANB=
|MN|•|x1-x2|=
|MN|•
=3•|MN|•
能求出椭圆C的方程.
(II)设直线MA、MB的方程分别为y=k1(x-2)+3(5)y=k2(x-2)+3(k1,2∈R),得:(16k12+12)x2+(96k1-64k12)x+64k12-192k1-48=0,得A(
,
),同理:B(
,
),所以
kAB=
=
=
,由此能够证明△MAB直角三角形.
| 1 |
| 2 |
| a2 |
| 4 |
| ma2 | ||
b2+
|
| ma2-a2b2 | ||
b2+
|
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| ||
b2+
|
(II)设直线MA、MB的方程分别为y=k1(x-2)+3(5)y=k2(x-2)+3(k1,2∈R),得:(16k12+12)x2+(96k1-64k12)x+64k12-192k1-48=0,得A(
| 8k12-24k1-6 |
| 4k12+3 |
| -12k12-12k1+9 |
| 4k12+3 |
| 8k22-24k2-6 |
| 4k22+3 |
| -12k22-12k2+9 |
| 4k22+3 |
kAB=
| y1-y2 |
| x1-x2 |
| ||||
|
| 1 |
| 2 |
解答:解:(I)设直线l的方程为y=
x+m(m∈R),
代入b2x2+a2y2=a2b2
得:(b2+
)x2+ma2x+a2m2-a2b2=0,
设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R)
则x1+x2=-
,x1•x2=
,------(3分)
又SMANB=
|MN|•|x1-x2|=
|MN|•
=3•|MN|•
,
显然当m=0时,SMANB=3•|MN|•
=12
(1)
由题意|MN|=6 (2)
4b2+9a2=a2b2(3)------(5分)
联立(1)、(2)、(3)解得:a2=16,b2=12,
即椭圆C的方程为:
+
=1.(4)------(7分)
(II)设直线MA、MB的方程分别为y=k1(x-2)+3(5)y=k2(x-2)+3(k1,2∈R)
将(5)代入(4)得:(16k12+12)x2+(96k1-64k12)x+64k12-192k1-48=0------(9分)
则2x1=
,
∴x1=
∴A(
,
)
同理:B(
,
)
kAB=
=
=
------(12分)
化简得:k12=k22,
∵k1≠k2,
∴k1=-k2
即直线MA与MB关于直线MN对称,
∴∠AMN=∠BMN------(14分)
∴N到直线MA与MB距离均为3
,
又|MN|=6,
∴∠AMN=∠BMN=
,
∴∠AMB=
.
故△MAB直角三角形.------(15分)
| 1 |
| 2 |
代入b2x2+a2y2=a2b2
得:(b2+
| a2 |
| 4 |
设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R)
则x1+x2=-
| ma2 | ||
b2+
|
| ma2-a2b2 | ||
b2+
|
又SMANB=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
=3•|MN|•
| ||
b2+
|
显然当m=0时,SMANB=3•|MN|•
| ||
b2+
|
| 3 |
由题意|MN|=6 (2)
4b2+9a2=a2b2(3)------(5分)
联立(1)、(2)、(3)解得:a2=16,b2=12,
即椭圆C的方程为:
| x2 |
| 16 |
| y2 |
| 12 |
(II)设直线MA、MB的方程分别为y=k1(x-2)+3(5)y=k2(x-2)+3(k1,2∈R)
将(5)代入(4)得:(16k12+12)x2+(96k1-64k12)x+64k12-192k1-48=0------(9分)
则2x1=
| 64k12-192k1-48 |
| 16k12+12 |
∴x1=
| 8k12-24k1-6 |
| 4k12+3 |
∴A(
| 8k12-24k1-6 |
| 4k12+3 |
| -12k12-12k1+9 |
| 4k12+3 |
同理:B(
| 8k22-24k2-6 |
| 4k22+3 |
| -12k22-12k2+9 |
| 4k22+3 |
kAB=
| y1-y2 |
| x1-x2 |
| ||||
|
| 1 |
| 2 |
化简得:k12=k22,
∵k1≠k2,
∴k1=-k2
即直线MA与MB关于直线MN对称,
∴∠AMN=∠BMN------(14分)
∴N到直线MA与MB距离均为3
| 2 |
又|MN|=6,
∴∠AMN=∠BMN=
| π |
| 4 |
∴∠AMB=
| π |
| 2 |
故△MAB直角三角形.------(15分)
点评:本题主要椭圆方程的求法,判断三角形的形状.解题时要熟练掌握椭圆的简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力.综合性强,是高考的重点,易错点是椭圆的知识体系不牢固.解题时要认真审题,注意化归与转化思想的灵活运用.

练习册系列答案
相关题目
 (2010•台州二模)一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是球体的一部分,则这个几何体的表面积为
(2010•台州二模)一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是球体的一部分,则这个几何体的表面积为