Question

【题目】定义符号函数，已知函数.

（1）已知，求实数的取值集合；

（2）当时，在区间上有唯一零点，求的取值集合；

（3）已知在上的最小值为，求正实数的取值集合；

Answer 1

【答案】（1）；（2）；（3）；

【解析】

（1）先求出的表达式，再解关于的不等式，从而求得的值；

（2）当时，写出函数解析式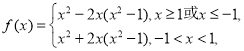，再将问题转化为函数与在区间上有唯一的交点，作出图象，即可得到答案；

（3）由题意得，，再对分和两种情况讨化，对的情况，再进行二级讨论，即和两种情况，最后进行综合得到正实数的取值集合.

（1）因为，

所以或

解得：或，

所以实数的取值集合为.

（2）当时，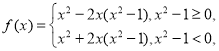

所以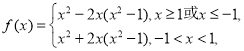

因为在区间上有唯一零点，

所以方程在区间上有唯一的根，

所以函数与在区间上有唯一的交点，

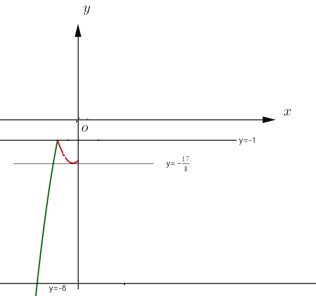
函数的图象，如图所示：

当或时，两个函数图象只有一个公共点，

所以的取值集合为时，在区间上有唯一零点.

（3）当时，在恒成立，

因为，，

①当时，，

所以在恒成立，

所以.

②当时，，

ⅰ）当时，上式，

所以在恒成立，

所以，此时的数都成立；

ⅱ）当时，，

所以在恒成立，

当，即时，，

所以；

当，即时，，

所以；

所以；

综合①②可得：或，

所以正实数的取值集合为：.