题目内容
【题目】郴州某超市计划按月订购一种饮料,每天进货量相同,进货成本每瓶6元,售价每瓶8元,未售出的饮料降价处理,以每瓶3元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种饮料一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种饮料的利润为Y(单位:元),当六月份这种饮料一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
【答案】(2)详见解析;(2)![]() 时,
时,![]() 的数学期望达到最大值,最大值为
的数学期望达到最大值,最大值为![]() 元.
元.
【解析】
(1)由题意知![]() 的可能取值为200,300,500,分别求出相应的概率,由此能求出
的可能取值为200,300,500,分别求出相应的概率,由此能求出![]() 的分布列.
的分布列.
(2)由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,只需考虑![]() ,根据
,根据![]() 和
和![]() 分类讨论,能得到当
分类讨论,能得到当![]() 时,
时,![]() 最大值为520元.
最大值为520元.
解:(1)由题意知![]() 的可能取值为200,300,500,
的可能取值为200,300,500,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列为:
的分布列为:
| 200 | 300 | 500 |
| 0.2 | 0.4 | 0.4 |
(2)由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,
![]() 只需考虑
只需考虑
当![]() 时,
时,
若最高气温不低于25,则![]() ;
;
若最高气温位于区间![]() ,
,![]() ,则
,则![]() ;
;
若最高气温低于20,则![]() ,
,
![]() ,
,
当![]() 时,
时,
若最高气温不低于20,则![]() ,
,
若最高气温低于20,则![]() ,
,
![]() .
.
![]() 时,
时,![]() 的数学期望达到最大值,最大值为
的数学期望达到最大值,最大值为![]() 元.
元.

【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: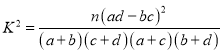 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |