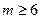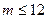题目内容
(本题满分12分)
设函数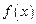 的定义域为
的定义域为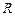 ,当
,当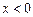 时,
时,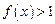 ,且对任意的实数
,且对任意的实数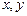 ,有
,有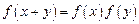 .
.
(Ⅰ)求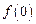 ,判断并证明函数
,判断并证明函数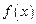 的单调性;
的单调性;
(Ⅱ)数列 满足
满足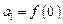 ,且
,且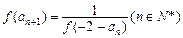
①求通项公式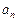 的表达式;
的表达式;
②令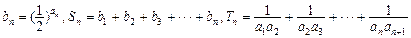 ,试比较
,试比较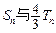 的大小,并加以证明.
的大小,并加以证明.
设函数
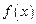 的定义域为
的定义域为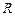 ,当
,当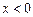 时,
时,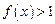 ,且对任意的实数
,且对任意的实数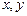 ,有
,有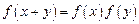 .
.(Ⅰ)求
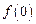 ,判断并证明函数
,判断并证明函数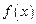 的单调性;
的单调性;(Ⅱ)数列
 满足
满足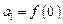 ,且
,且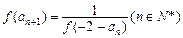
①求通项公式
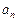 的表达式;
的表达式;②令
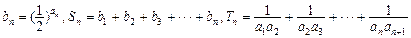 ,试比较
,试比较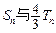 的大小,并加以证明.
的大小,并加以证明.①
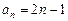

②

(Ⅰ)令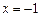 ,
, 得
得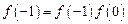 ,
,
又 ,
,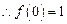 ……2分
……2分

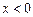 时,
时,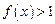 ,
,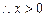 时,
时,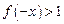 ,此时
,此时
 对
对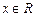 ,
,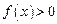 . ……3分
. ……3分
设 ,
,
即 ,故
,故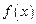 在
在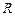 是减函数. ……5分
是减函数. ……5分
(Ⅱ)由
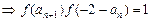

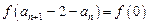
而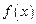 单调,
单调,
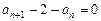 ,即
,即


 是以2为公差的等差数列,
是以2为公差的等差数列,
 ,
,
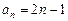
 .……8分
.……8分
故 ,
, 是以
是以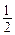 为首项,
为首项,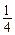 为公比的等比数列.
为公比的等比数列.




 ……10分
……10分
要比较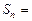
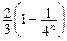 与
与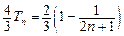 的大小,只要比较
的大小,只要比较 和
和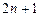 的大小.
的大小.
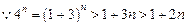 ,
, . ……12分
. ……12分
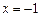 ,
, 得
得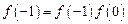 ,
,又
 ,
,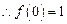 ……2分
……2分
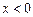 时,
时,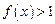 ,
,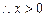 时,
时,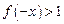 ,此时
,此时
 对
对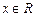 ,
,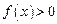 . ……3分
. ……3分设
 ,
,
即
 ,故
,故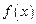 在
在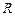 是减函数. ……5分
是减函数. ……5分(Ⅱ)由

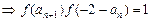

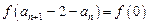
而
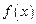 单调,
单调,
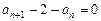 ,即
,即


 是以2为公差的等差数列,
是以2为公差的等差数列,
 ,
,
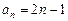
 .……8分
.……8分故
 ,
, 是以
是以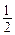 为首项,
为首项,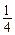 为公比的等比数列.
为公比的等比数列.



 ……10分
……10分要比较
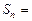
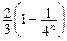 与
与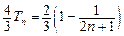 的大小,只要比较
的大小,只要比较 和
和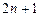 的大小.
的大小.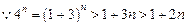 ,
, . ……12分
. ……12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 对边分别为
对边分别为 ,且
,且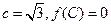 ,若
,若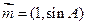 与
与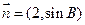 共线,求
共线,求 的值.
的值.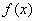 是定义在
是定义在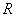 的增函数,且
的增函数,且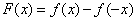 ,那么
,那么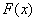 一定是( )
一定是( ) 在
在 上是增函数,函数
上是增函数,函数 是偶函数,则
是偶函数,则 大小关系为_________________________.
大小关系为_________________________.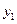 与时间t满足关系式:
与时间t满足关系式: ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度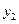 与时间t满足关系式:
与时间t满足关系式: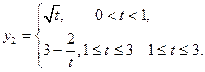 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。 上的偶函数, 且在( 0 , +
上的偶函数, 且在( 0 , +  )上是减函数,如果
)上是减函数,如果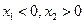 ,且
,且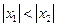 ,则有( )
,则有( )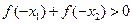
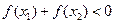
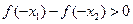
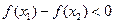
 ,有下列四个命题:
,有下列四个命题: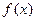 是奇函数; ②
是奇函数; ②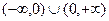 ;
;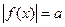 总有四个不同的解;④
总有四个不同的解;④ 在区间
在区间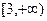 上为单调增函数,则
上为单调增函数,则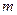 的取值范围为( )
的取值范围为( )