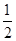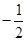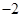题目内容
已知函数 ,
, 的图象经过
的图象经过 和
和 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
的值域为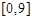 .过该函数图象上的动点
.过该函数图象上的动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 .
.

(I)求函数 的解析式;
的解析式;
(Ⅱ)记 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
 ,
, 的图象经过
的图象经过 和
和 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
的值域为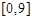 .过该函数图象上的动点
.过该函数图象上的动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 .
.
(I)求函数
 的解析式;
的解析式;(Ⅱ)记
 的面积为
的面积为 ,求
,求 的最大值.
的最大值.(I)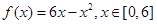 ;(II)三角形面积的最大值为16.
;(II)三角形面积的最大值为16.
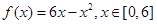 ;(II)三角形面积的最大值为16.
;(II)三角形面积的最大值为16.试题分析:(I)用待定系数法.由抛物线的对称性及题设可知,函数
 的对称轴为
的对称轴为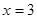 ,顶点为
,顶点为 .
.将顶点坐标及点(0,0),(0,6)的坐标代入解析式得关于a,b,c方程组,解此方程组,便可得
 的解析式.
的解析式. (II)用三角形面积公式求得三角形的面积与t之间的函数关系式,然后利用导数可求得
 的面积为
的面积为 ,求
,求 的最大值.
的最大值.试题解析:(I)由已知可得函数
 的对称轴为
的对称轴为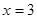 ,顶点为
,顶点为 . 2分
. 2分方法一:由

得
 5分
5分得
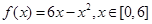 6分
6分方法二:设
 4分
4分由
 ,得
,得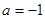 5分
5分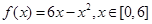 6分
6分(II)
 8分
8分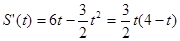 9分
9分 列表得:
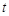 | 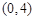 | 4 |  |
 | + | 0 | - |
 |  | 极大值 |  |
由上表可得
 时,三角形面积取得最大值
时,三角形面积取得最大值 即
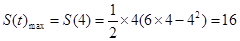 13分
13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.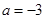 ,
,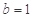 时,求函数
时,求函数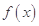 的最大值;
的最大值;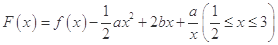 ,其图象上存在一点
,其图象上存在一点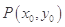 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数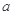 的取值范围;
的取值范围; ,
,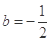 时,方程
时,方程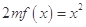 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.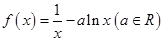 .
.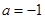 时,试确定函数
时,试确定函数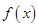 在其定义域内的单调性;
在其定义域内的单调性;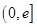 上的最小值;
上的最小值;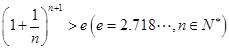 .
. .
. 的单调区间;
的单调区间; 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; (
( 是自然对数的底数)使
是自然对数的底数)使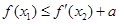 ,求实数
,求实数

 在
在 处的切线垂直
处的切线垂直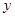 轴,求
轴,求 的值;
的值; 上为增函数,求
上为增函数,求 的单调性.
的单调性. ,(其中m为常数).
,(其中m为常数).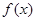 在区间
在区间 上的单调性;
上的单调性; .当
.当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 、
、 ,使得过
,使得过 、
、 点处的切线互相平行,求
点处的切线互相平行,求 的取值范围.
的取值范围. -
-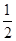 alnx,a∈R.
alnx,a∈R.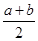 )≤
)≤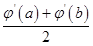 ≤φ′(
≤φ′(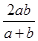 ).
).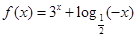 的零点所在区间为( )
的零点所在区间为( )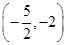
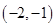

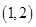
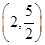
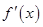 是函数
是函数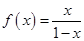 的导数,则
的导数,则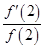 的值是( )
的值是( )