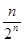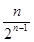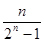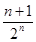题目内容
已知数列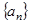 的各项均是正数,其前
的各项均是正数,其前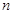 项和为
项和为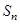 ,满足
,满足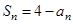 .
.
(I)求数列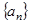 的通项公式;
的通项公式;
(II)设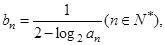 数列
数列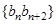 的前
的前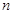 项和为
项和为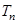 ,求证:
,求证: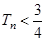 .
.
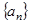 的各项均是正数,其前
的各项均是正数,其前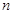 项和为
项和为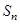 ,满足
,满足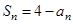 .
.(I)求数列
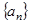 的通项公式;
的通项公式;(II)设
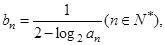 数列
数列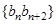 的前
的前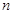 项和为
项和为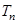 ,求证:
,求证: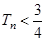 .
.(Ⅰ)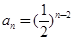 . (Ⅱ)详见解析.
. (Ⅱ)详见解析.
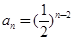 . (Ⅱ)详见解析.
. (Ⅱ)详见解析. 试题分析:(Ⅰ)首先令
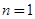 求出首项
求出首项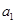 ,
,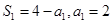 .
. 由
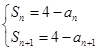 两式相减,得
两式相减,得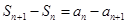 即
即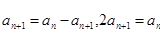 .所以
.所以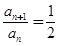 ,
,数列
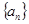 是首项为2,公比为
是首项为2,公比为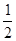 的等比数列.由等比数列的通项公式便可得数列
的等比数列.由等比数列的通项公式便可得数列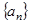 的通项公式.
的通项公式.(Ⅱ)证明有关数列前
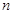 项和的不等式,一般有以下两种思路:一种是先求和后放缩,一种是先放缩后求和.在本题中,由(Ⅰ)可得:
项和的不等式,一般有以下两种思路:一种是先求和后放缩,一种是先放缩后求和.在本题中,由(Ⅰ)可得: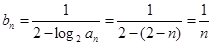 ,
,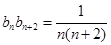 .这显然用裂项法求和,然后用放缩法即可证明.
.这显然用裂项法求和,然后用放缩法即可证明.试题解析:(Ⅰ)由题设知
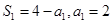 , 2分
, 2分由
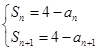 两式相减,得
两式相减,得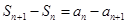 .
.所以
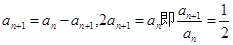 . 4分
. 4分可见,数列
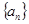 是首项为2,公比为
是首项为2,公比为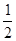 的等比数列。
的等比数列。所以
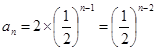 6分
6分(Ⅱ)
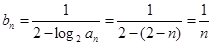 , 8分
, 8分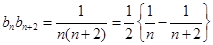 . 10分
. 10分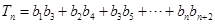
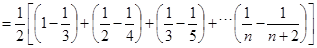
=
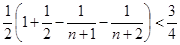 . 12分
. 12分
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
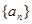 ,
,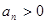 ,
,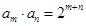 ,
,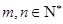 .
.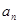 ;
;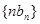 的前
的前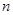 项和为
项和为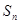 且
且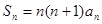 ,求
,求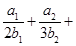
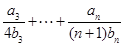 .
.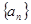 的前
的前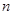 项的和为
项的和为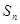 ,点
,点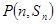
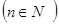 在函数
在函数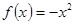
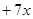 的图象上.
的图象上.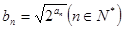 ,求数列
,求数列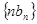 的前
的前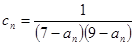 ,数列
,数列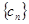 的前
的前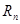 ,求使不等式
,求使不等式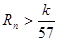 对一切
对一切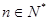 都成立的最大正整数
都成立的最大正整数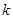 的值.
的值.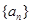 有无穷多项,各项均为正数,前
有无穷多项,各项均为正数,前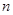 项和为
项和为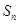 ,
,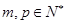 ,且
,且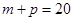 ,
,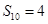 ,则
,则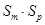 的最大值为 .
的最大值为 .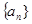 ,那么
,那么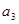 的所有可能取值中最小的是( )
的所有可能取值中最小的是( ) 的公差
的公差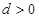 ,若
,若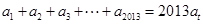 (
( ),则
),则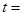 ( )
( )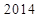
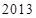
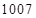
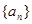 的前
的前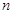 项和是
项和是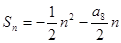 ,则使
,则使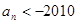 的最小正整数
的最小正整数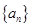 的前
的前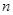 项和
项和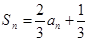 ,则数列
,则数列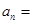 ( )
( )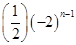
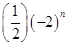
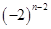
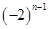
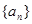 中,
中,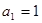 ,2
,2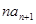 =
=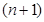
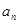 ,则数列
,则数列