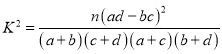题目内容
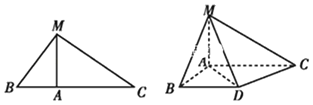
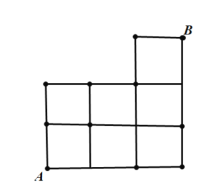
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AB的中点
,E为AB的中点![]() 将
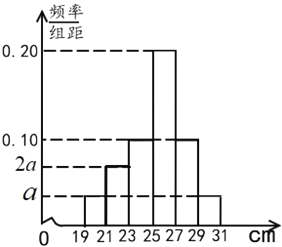
将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
![]() 求证:平面
求证:平面![]() 平面AEF;
平面AEF;
![]() 求直线DF与平面CEF所成角的正弦值.
求直线DF与平面CEF所成角的正弦值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由题意可得![]() 故
故![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]()
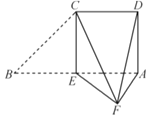
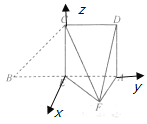
(2) 以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴的正方向建立如图所示空间直角坐标系
轴的正方向建立如图所示空间直角坐标系![]() 求出
求出![]() 及平面
及平面![]() 的法向量,代入公式可得结果.
的法向量,代入公式可得结果.
证明:![]() 在直角梯形
在直角梯形![]() 中,由平面几何的知识,得四边形
中,由平面几何的知识,得四边形![]() 为正方形,
为正方形,
则![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
解:![]() 由
由![]() 得
得![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]()
![]() .
.
又![]() ,所以
,所以![]() 为正三角形.
为正三角形.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴的正方向建立如图所示空间直角坐标系
轴的正方向建立如图所示空间直角坐标系![]()
则![]()
从而![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则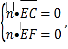 即
即![]()
![]() ,得
,得![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
则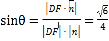
∴直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.

【题目】进入21世纪,互联网和通讯技术高速发展使商务进入一个全新的阶段,网上购物这一方便、快捷的购物形式已经被越来越多的人所接受![]() 某互联网公司为进一步了解大学生的网上购物的情况,对大学生的消费金额进行了调查研究,得到如下统计表:
某互联网公司为进一步了解大学生的网上购物的情况,对大学生的消费金额进行了调查研究,得到如下统计表:
组数 | 消费金额 | 人数 | 频率 |
第一组 |
| 1100 |
|
第二组 |
| 3900 |
|
第三组 |
| 3000 | p |
第四组 |
| 1200 |
|
第五组 | 不低于200元 | m |
|
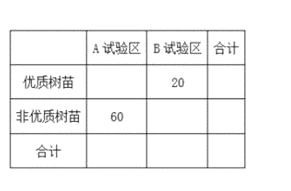
![]() 求m,p的值;
求m,p的值;
![]() 该公司从参与调查且购物满150元的学生中采用分层抽样的方法抽取
该公司从参与调查且购物满150元的学生中采用分层抽样的方法抽取![]() 作为中奖用户,再随机抽取中奖用户的
作为中奖用户,再随机抽取中奖用户的![]() 获得一等奖
获得一等奖![]() 求第五组至少1人获得一等奖的概率.
求第五组至少1人获得一等奖的概率.
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成![]() ,
,![]() 两组,每组20人,
两组,每组20人,![]() 组群众给第一阶段的创文工作评分,
组群众给第一阶段的创文工作评分,![]() 组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
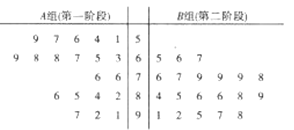
(Ⅰ)根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度(不要求计算出具体值,给出结论即可);
(Ⅱ)完成下面的列联表,并通过计算判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |