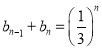题目内容
【题目】已知函数![]()
(1)求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若关于![]() 的不等式
的不等式![]() 有且只有三个整数解,求实数
有且只有三个整数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数f(x)在闭区间上的最小值即可;
(2)根据f(x)的单调性,通过讨论n的符号,解关于f(x)的不等式结合不等式解的个数,求出n的范围即可.
解:(1)![]() ,令
,令![]() ,得
,得![]() 的递增区间为
的递增区间为![]() ;令
;令![]() ,得
,得![]() 的递减区间为
的递减区间为![]()
![]() ,则当
,则当![]() 时,
时,![]() 在
在![]() 上为增函数,
上为增函数,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,又
上为减函数,又![]() ,
,
![]() 若
若![]() ,
,![]() 的最小值
的最小值![]() ,若
,若![]() ,
,![]() 的最小值为
的最小值为![]() ,
,
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;若
;若![]() ,
,![]() 的最小值为
的最小值为![]()
(2)由(1)知,![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ,且在
,且在![]() 上,
上,![]() ,又
,又![]() ,则
,则![]() ,又
,又![]() 时,由不等式
时,由不等式![]() 得
得![]() 或
或![]() ,而
,而![]() 的解集为
的解集为![]() ,整数解有无数多个,不合题意;
,整数解有无数多个,不合题意;
![]() 时,由不等式
时,由不等式![]() ,得
,得![]() ,解集为
,解集为![]() ,整数解有无数多个,不合题意;
,整数解有无数多个,不合题意;
![]() 时由不等式
时由不等式![]() ,得
,得![]() 或
或![]() ,
,![]() 的解集为
的解集为![]() 无整数解,若不等式
无整数解,若不等式![]() 有且只有三个整数解,
有且只有三个整数解,![]() 在
在![]() 递增,在
递增,在![]() 递减,而
递减,而![]() ,而
,而![]() ,所以,三个正整数1,2,3,而
,所以,三个正整数1,2,3,而![]() ,综上,实数
,综上,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
(相关公式: )
)