题目内容
若f（x）=x2-bx+c，且f（1）=0，f（2）=0，则f（4）=
- A.-8
- B.-6
- C.6
- D.8
C
分析：利用已知的两个函数值列出关于b，c的方程组求出b，c，求出该二次函数的表达式之后，让自变量x取4求出所求的函数值．
解答：∵f（x）=x2-bx+c，且f（1）=0，f（2）=0
∴
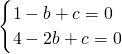解得
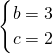
即f（x）=x2-3x+2
∴f（4）=42-3×4+2=6
故选C．
点评：本题考查函数解析式求解的待定系数法，考查方程求未知数的思想，属于基础题．
分析：利用已知的两个函数值列出关于b，c的方程组求出b，c，求出该二次函数的表达式之后，让自变量x取4求出所求的函数值．
解答：∵f（x）=x2-bx+c，且f（1）=0，f（2）=0
∴
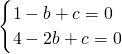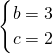
解得即f（x）=x2-3x+2
∴f（4）=42-3×4+2=6
故选C．
点评：本题考查函数解析式求解的待定系数法，考查方程求未知数的思想，属于基础题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
若 f（x）=-x2+2ax 与g（x）=
在区间[1，2]上都是减函数，则a的取值范围是（ ）
| a |
| x+1 |
| A、（-1，0）∪（0，1） |
| B、（-1，0）∪（0，1] |
| C、（0，1] |
| D、（0，1） |