题目内容
如图,点C是以AB为直径的圆上的一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE= BC.
BC.

(1)证明:EO∥平面ACD;
(2)证明:平面ACD⊥平面BCDE.
 BC.
BC.
(1)证明:EO∥平面ACD;
(2)证明:平面ACD⊥平面BCDE.
(1)见解析(2)见解析
(1)如图,取BC的中点M,连结OM、ME.
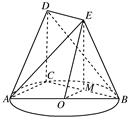
在△ABC中,O为AB的中点,M为BC的中点,∴OM∥AC,
在直角梯形BCDE中,DE∥BC,且DE= BC=CM,
BC=CM,
∴四边形MCDE为平行四边形,∴EM∥DC,
∴面EMO∥面ACD,
又∵EO?面EMO,
∴EO∥面ACD.
(2)∵C在以AB为直径的圆上,∴AC⊥BC,
又∵面BCDE⊥面ABC,面BCDE∩面ABC=BC,
∴AC⊥面BCDE,
又∵AC?面ACD,
∴面ACD⊥面BCDE.

在△ABC中,O为AB的中点,M为BC的中点,∴OM∥AC,
在直角梯形BCDE中,DE∥BC,且DE=
 BC=CM,
BC=CM,∴四边形MCDE为平行四边形,∴EM∥DC,
∴面EMO∥面ACD,
又∵EO?面EMO,
∴EO∥面ACD.
(2)∵C在以AB为直径的圆上,∴AC⊥BC,
又∵面BCDE⊥面ABC,面BCDE∩面ABC=BC,
∴AC⊥面BCDE,
又∵AC?面ACD,
∴面ACD⊥面BCDE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
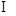 β,且α⊥β,则l⊥α;
β,且α⊥β,则l⊥α;
 A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )