题目内容
16.已知函数f(x)=(ax-b)ex(a≠0).①若f(x)≥f(0)恒成立,求f(1)的值;
②f(x)在(a,+∞)是单调减函数,求b的取值范围.
分析 ①若f(x)≥-b恒成立,转化为求函数的最小值即可求f(1)的值;
②f(x)在(a,+∞)是单调减函数,则f′(x)≤0成立,即可求b的取值范围.
解答 解:①注意到f(0)=-b,故f(x)≥f(0)恒成立,故f(x)在x=0处取得最小值.
而f′(x)=(ax+a-b)ex,
由f′(x)=0得ax+a-b=0的根为x=0(此时a>0),
则a-b=0,f(1)=(a-b)e=0.…(6分)
②由①知f′(x)=(ax+a-b)ex,
当a>0时,由f′(x)<0解得x<$\frac{b-a}{a}$,
故f(x)在(-∞,$\frac{b-a}{a}$)上递减,矛盾;则a<0,
由f′(x)<0解得x>$\frac{b-a}{a}$,故a≥$\frac{b-a}{a}$,
b≤a2+a=(a+$\frac{1}{2}$)2-$\frac{1}{4}$,
因此b≤-$\frac{1}{4}$.…(12分)
点评 本题主要考查函数的单调性的应用,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
7.函数y=ln(x+1)与y=$\frac{a}{x}$的图象的一个交点的横坐标所在区间为(1,2),则实数a的取值范围是( )
| A. | (-∞,2ln3) | B. | (ln2,2ln3) | C. | (ln2,+∞) | D. | (-∞,2ln3)∪(ln2,+∞) |
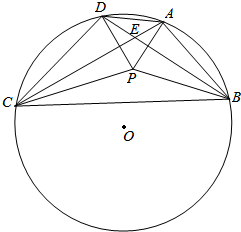 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.