题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
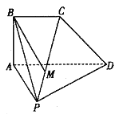
(1)证明:![]() ;
;
(2)设点M在线段PC上,且![]() ,若
,若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据面面垂直的性质可证明![]() 平面PAD,再证明
平面PAD,再证明![]() 平面PAB. 即可证明
平面PAB. 即可证明![]() .
.
(2) 设![]() ,再根据
,再根据![]() 与
与![]() 的面积为
的面积为![]() 可得
可得![]() ,解得
,解得![]() .再根据等面积法求得 P到AD的距离
.再根据等面积法求得 P到AD的距离![]() ,进而求得四棱锥
,进而求得四棱锥![]() 的体积即可.
的体积即可.
(1)证明:因为![]() ,所以
,所以![]() .
.
因为平面![]() 平面PAD,交线为AD,
平面PAD,交线为AD,
所以![]() 平面PAD,从而
平面PAD,从而![]()
又![]() ,故
,故![]() ,
,
因为![]() ,所以
,所以![]() 平面PAB.
平面PAB.
又PB![]() 平面PAB,所以
平面PAB,所以![]() .
.
(2)设![]() ,则
,则![]() ,
,![]() .
.
由(1)知![]() 平面PAD,所以
平面PAD,所以![]() ,
,![]() ,
,
取AD中点为F,连接CF,PF,则![]() ,
,![]() .
.
由(1)知![]() 平面PAD,所以
平面PAD,所以![]() 平面PAD,所以
平面PAD,所以![]() ,
,
又因为![]() ,所以
,所以![]()
又因为![]() ,所以
,所以![]() ,
,
所以![]()
由![]() ,解得
,解得![]() .
.
在![]() 中,
中,![]() ,
,
P到AD的距离![]() ,
,
所以![]() 到平面ABCD的距离
到平面ABCD的距离![]() ,
,
故![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.