Question

【题目】判定下列函数的奇偶性．

（1）f（x）＝；

（2）f（x）＝；

（3）f（x）＝；

（4）f（x）＝|x＋1|＋|x－1|.

Answer 1

【答案】（1）非奇非偶函数，（2）既是奇函数又是偶函数，

（3）奇函数，（4）偶函数

【解析】（1）f（x）的定义域是（－∞，1）∪（1，＋∞），不关于原点对称，∴f（x）是非奇非偶函数.

（2）f（x）的定义域是{－1,1}，关于原点对称，且f（－1）＝f（1）＝0，∴f（－1）＝f（1），且

f（－1）＝－f（1），

∴函数f（x）既是奇函数又是偶函数.

（3）f（x）的定义域为（－∞，＋∞），关于原点对称，

又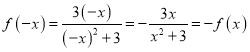，∴f（x）是奇函数.

（4）f（x）的定义域为R，

又f（－x）＝|－x＋1|＋|－x－1|＝|x－1|＋|x＋1|＝f（x），

∴f（x）是偶函数．