题目内容
若关于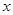 的方程
的方程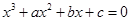 的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则
的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则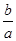 的取值范围为 .
的取值范围为 .
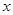 的方程
的方程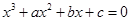 的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则
的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则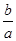 的取值范围为 .
的取值范围为 . 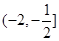
试题分析:令f(x)=x3+ax2+bx+c
∵抛物线的离心率为1,∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
∴c=-1-a-b代入f(x)=x3+ax2+bx+c,
可得f(x)=x3+ax2+bx-1-a-b=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b,则g(x)=0的两根满足0<x1<1,x2>1
∴g(0)=1+a+b>0,g(1)=3+2a+b<0
作出可行域,如图所示
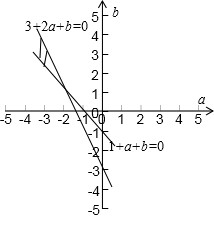
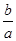 的几何意义是区域内的点与原点连线的斜率,
的几何意义是区域内的点与原点连线的斜率,∴-2≤
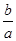 <-
<-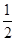 故答案为:-2≤
故答案为:-2≤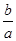 <-
<-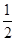
点评:解题的关键是根据条件来写出不等式组,然后结合规划知识来得到。涉及到了函数的根的分布,多项式恒等等知识.属中档题。

练习册系列答案
相关题目
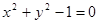 和
和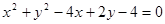 的位置关系是
的位置关系是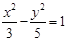 的左焦点F引圆
的左焦点F引圆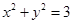 的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | = .
的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | = .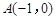 ,
,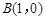 ,△
,△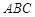 的周长为6.
的周长为6.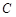 的轨迹
的轨迹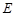 的方程;
的方程;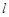 与曲线
与曲线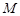 ,
,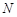 .若点
.若点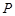 在
在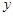 轴上,且
轴上,且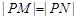 ,求点
,求点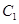 的方程为
的方程为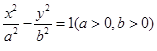 ,
,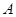 、
、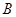 为其左、右两个顶点,
为其左、右两个顶点, 是双曲线
是双曲线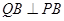 ,
,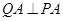 ,垂足分别为
,垂足分别为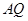 与
与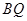 交于点
交于点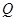 .
.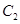 方程;
方程;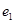 、
、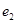 ,当
,当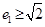 时,求
时,求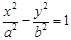 (a>0,b>0)的左、右焦点,过F1的直线
(a>0,b>0)的左、右焦点,过F1的直线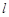 与
与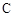 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为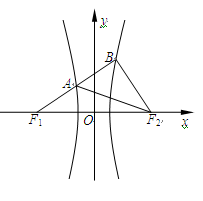
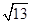
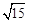
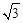
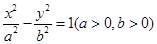 的一条渐近线与直线
的一条渐近线与直线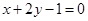 垂直,则曲线的离心率等于 。
垂直,则曲线的离心率等于 。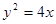 的焦点为F,准线为l,点P为抛物线上一点,且
的焦点为F,准线为l,点P为抛物线上一点,且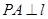 ,垂足为A,若直线AF的斜率为
,垂足为A,若直线AF的斜率为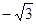 ,则|PF|等于( )
,则|PF|等于( )