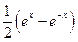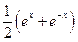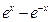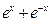题目内容
已知函数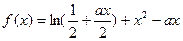
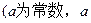 >0)
>0)
(1)若 的一个极值点,求
的一个极值点,求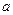 的值;
的值;
(2)求证:当0<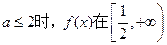 上是增函数;
上是增函数;
(3)若对任意的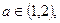 总存在
总存在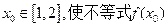 >
>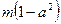 成立,求实数m的取值范围。
成立,求实数m的取值范围。
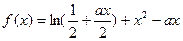
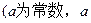 >0)
>0)(1)若
 的一个极值点,求
的一个极值点,求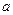 的值;
的值;(2)求证:当0<
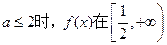 上是增函数;
上是增函数;(3)若对任意的
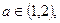 总存在
总存在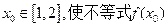 >
>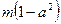 成立,求实数m的取值范围。
成立,求实数m的取值范围。

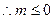 时不可能使
时不可能使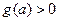 恒成立,故必有
恒成立,故必有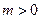
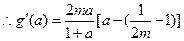 .
.若
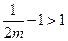 ,可知
,可知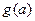 在区间
在区间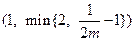 上递减,
上递减,在此区间上,有
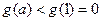 ,与
,与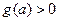 恒成立矛盾,
恒成立矛盾,故
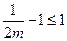 ,这
,这 时,
时,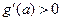 ,
,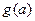
 在
在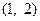 上递增,
上递增,恒有
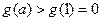 ,满足题
,满足题 设要求,
设要求,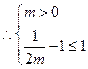 ,即
,即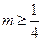 ,
,所以,实数
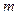 的取值范围为
的取值范围为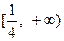 .
. 略

练习册系列答案
相关题目
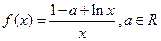 .
.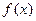 的极值;
的极值;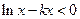 在
在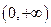 上恒成立,求
上恒成立,求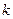 的取值范围;
的取值范围;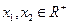 ,且
,且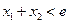 ,求证:
,求证: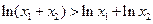 .
.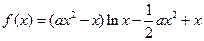 .
.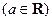 .
.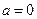 时,求曲线
时,求曲线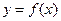 在
在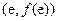 处的切线方程(
处的切线方程(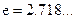 );
);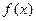 的单调区间.
的单调区间.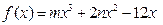 的减区间是
的减区间是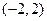 .
.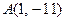 且与曲线
且与曲线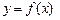 相切的切线方程;
相切的切线方程;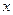 艘的产值函数为
艘的产值函数为 (单位:万元),成本函数为
(单位:万元),成本函数为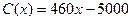 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数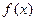 的边际函数
的边际函数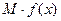 定义为
定义为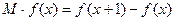 。
。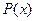 及边际利润函数
及边际利润函数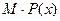 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)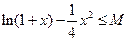 恒成立,则
恒成立,则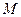 的最小值为 .
的最小值为 . 
 函数
函数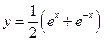 的导数是( )
的导数是( )