题目内容
1.设函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x),f(7-x)=f(7+x),若f(-2)=0,则f(2008)=0.分析 利用已知条件求出函数的对称轴,函数的周期,然后求解函数值即可.
解答 解:函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x),函数关于x=2对称,
f(7-x)=f(7+x),函数关于x=7对称,所以函数的周期为5,
f(-2)=0,则f(2008)=f(5×402-2)=f(-2)=0.
故答案为:0.
点评 本题考查抽象函数的应用,函数的周期性,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在一个文艺比赛中,12名专业人士和12名观众代表各组成一个评判小组,给参赛选手打分.下面是两个评判组对同一名选手的打分:
(1)解释如何衡量每一组成员的相似性.
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
| 小组A | 42 | 45 | 48 | 46 | 52 | 47 | 49 | 55 | 42 | 51 | 47 | 45 |
| 小组B | 55 | 36 | 70 | 66 | 75 | 49 | 46 | 68 | 42 | 62 | 58 | 47 |
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
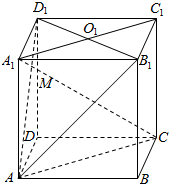 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.
如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.