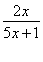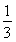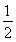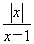题目内容
已知函数f(x)=ax2-|x|+2a-1(a为实常数).
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设h(x)=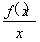 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
(1)
(2)g(a)= (3)
(3)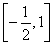
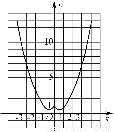
【解析】(1)当a=1时,f(x)=x2-|x|+1= 作图如下.
作图如下.

(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,g(a)=f(2)=-3.
若a≠0,则f(x)=a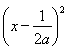 +2a-
+2a-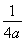 -1,f(x)图象的对称轴是直线x=
-1,f(x)图象的对称轴是直线x=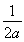 .
.
当a<0时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
当0<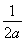 <1,即a>
<1,即a>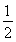 时,f(x)在区间[1,2]上是增函数,g(a)=f(1)=3a-2.
时,f(x)在区间[1,2]上是增函数,g(a)=f(1)=3a-2.
当1≤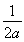 ≤2,即
≤2,即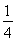 ≤a≤
≤a≤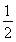 时,g(a)=f
时,g(a)=f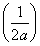 =2a-
=2a-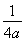 -1.
-1.
当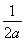 >2,即0<a<
>2,即0<a<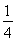 时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a-3.
综上可得g(a)=
(3)当x∈[1,2]时,h(x)=ax+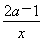 -1,在区间[1,2]上任取x1、x2,且x1<x2,
-1,在区间[1,2]上任取x1、x2,且x1<x2,
则h(x2)-h(x1)=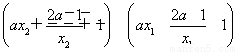
=(x2-x1) =(x2-x1)
=(x2-x1)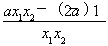 .
.
因为h(x)在区间[1,2]上是增函数,所以h(x2)-h(x1)>0.
因为x2-x1>0,x1x2>0,所以ax1x2-(2a-1)>0,
即ax1x2>2a-1.
当a=0时,上面的不等式变为0>-1,即a=0时结论成立.
当a>0时,x1x2>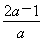 ,由1<x1x2<4,得
,由1<x1x2<4,得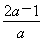 ≤1,解得0<a≤1.
≤1,解得0<a≤1.
当a<0时,x1x2<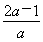 ,由1<x1x2<4,得
,由1<x1x2<4,得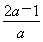 ≥4,解得-
≥4,解得-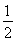 ≤a<0.
≤a<0.
所以实数a的取值范围为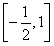

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目