题目内容

20．某厂生产甲产品每吨需用原料A和原料B分别为2吨和3吨，生产乙产品每吨需用原料A和原料B分别为2吨和1吨．甲、乙产品每吨可获利润分别为3千元和2千元．现有12吨原料A，8吨原料B．问计划生产甲产品和乙产品各多少吨才能使利润总额达到最大．

分析 首先由题意利用x，y满足的约束条件，以及目标函数，然后画出可行域，找到最优解求z是最值．

解答 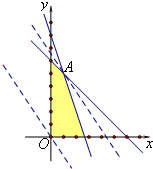解：计划生产甲产品和乙产品分别为x，y吨，则x，y满足的约束条件为为$\left\{\begin{array}{l}{x∈N，y∈N}\\{2x+2y≤12}\\{3x+y≤18}\end{array}\right.$，总利润z=3x+2y．…（4分）
约束条件如图所示，…（8分）
恰好在点A（1，5）处z取得最大值，即计划生产甲产品和乙产品分别为1吨和5吨能使得总利润最大．…（12分）

点评 本题考查了简单线性规划的应用；根据是明确题意，列出约束条件，根据约束条件画可行域，求目标函数的最值．

练习册系列答案
相关题目
10．设a＞0，b＞1，若a+b=2，则$\frac{2}{a}$+$\frac{1}{b-1}$的最小值为$3+2\sqrt{2}$．
11．已知x，y满足$\left\{\begin{array}{l}x≥1\\ x+y≤5\\ ax+by+c≤0\end{array}\right.$，记目标函数Z=2x+y的最大值为7，最小值为1，则a：b：c的值是2：（-3）：（-5）．
8．设$\overrightarrow{e_1}$，$\overrightarrow{e_2}$是两个不共线向量，若向量$\overrightarrow a=2\overrightarrow{e_1}-3\overrightarrow{e_2}$与向量$\overrightarrow b=3\overrightarrow{e_1}+λ\overrightarrow{e_2}$共线，则λ的值为（　　）
A．$\frac{2}{3}$B．-2C．$-\frac{9}{2}$D．$-\frac{2}{3}$
15．若等比数列前n项和为Sn，且满足S9=S6+S3，则公比q等于（　　）
A．1B．-1C．±1D．不存在
5．设函数${f_1}（x）=x\;，{f_2}（x）={log_{2016}}x\;，{a_i}=\frac{i}{2016}\;（\;i=1，\;\;\;2，\;\;\;…2016\;）$，记Ik=|fk（a2）-fk（a1）|+|fk（a3）-fk（a2）|+…+|fk（a2016）-fk（a2015）|，k=1，2，则（　　）
A．I1＜I2B．I1＞I2
C．I1=I2D．I1，I2大小关系不确定
12．三角形ABC满足，|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{AB}-\overrightarrow{AC}$|，点M为边BC的中点，且|$\overrightarrow{AM}$|=4，$\overrightarrow{AM}•（\overrightarrow{AB}-\overrightarrow{AC}）$=0，则边AC的长度为（　　）
A．4$\sqrt{2}$B．4C．8$\sqrt{2}$D．8
9．已知函数f（x）=2cosx（sinx-cosx）+1．
（1）求函数f（x）的最小正周期及单调增区间；
（2）画出函数y=f（x）在区间[0，π]内的图象；
（3）说明f（x）的图象可由y=sinx的图象经过怎样的变换得到的，并求f（x）在x∈[$\frac{5π}{24}$，$\frac{11π}{24}$]的值域．
10．某校数学课外小组在坐标纸上，为学校的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1=1，y1=1，当k≥2时，$\left\{\begin{array}{l}{x_k}={x_{k-1}}+1-5[{T（{\frac{k-1}{5}}）-T（{\frac{k-2}{5}}）}]\\{y_k}={y_{k-1}}+T（{\frac{k-1}{5}}）-T（{\frac{k-2}{5}}）\end{array}\right.$T（a）表示非负实数a的整数部分，例如T（2.6）=2，T（0.2）=0．按此方案，第2011棵树种植点的坐标应为（1，403）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网