题目内容
(本题满分16分)
已知函数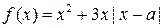 ,其中
,其中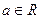 ,
,
(1)当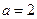 时,把函数
时,把函数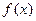 写成分段函数的形式;
写成分段函数的形式;
(2)当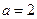 时,求
时,求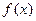 在区间
在区间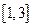 上的最值;
上的最值;
(3)设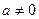 ,函数
,函数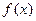 在
在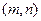 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出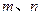 的取值范围(用
的取值范围(用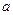 表示).
表示).
已知函数
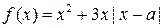 ,其中
,其中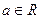 ,
,(1)当
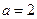 时,把函数
时,把函数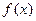 写成分段函数的形式;
写成分段函数的形式;(2)当
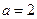 时,求
时,求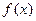 在区间
在区间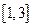 上的最值;
上的最值;(3)设
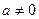 ,函数
,函数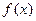 在
在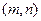 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出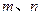 的取值范围(用
的取值范围(用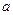 表示).
表示).解:(1)
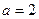 时,
时,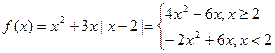 ……………………..4分
……………………..4分(2)结合图像,
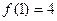 ,
,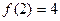 ,
,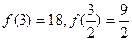
所以函数在区间
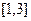 上最大值为18,最小值为4………..8分
上最大值为18,最小值为4………..8分(也可写出单调区间,写出可能的最值点及最值)

(3)当
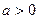 时,函数的图像如右,要使得在开区间
时,函数的图像如右,要使得在开区间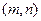 有最大值又有最小值,则最小值一定在
有最大值又有最小值,则最小值一定在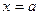 处取得,最大值在
处取得,最大值在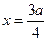 处取得;
处取得;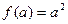 ,在区间
,在区间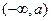 内,函数值为
内,函数值为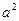 时
时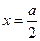 ,所以
,所以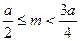 ;
;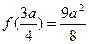 ,而在区间
,而在区间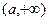 内函数值为
内函数值为 时
时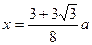 ,所以
,所以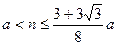 ……………..12分
……………..12分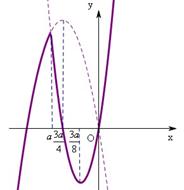
当
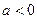 时,函数的图像如右,要使得在开区间
时,函数的图像如右,要使得在开区间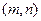 有最大值又有最小值,则最大值一定在
有最大值又有最小值,则最大值一定在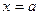 处取得,最小值在
处取得,最小值在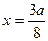 处取得,
处取得,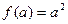 ,在
,在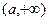 内函数值为
内函数值为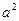 时
时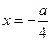 ,所以
,所以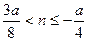 ,
,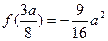 ,在区间
,在区间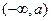 内,函数值为
内,函数值为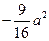 时,
时,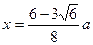 ,所以
,所以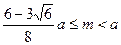 ……………..15分
……………..15分综上所述,
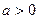 时,
时,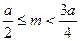 ,
,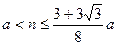 ;
;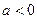 时,
时,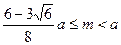 ,
,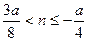 ……………………..16分
……………………..16分略

练习册系列答案
相关题目
 ,
, ,
, ,实数a满足
,实数a满足 >0,那么当x>1时必有( )
>0,那么当x>1时必有( ) <
< <
<
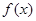 唯一的零点在区间
唯一的零点在区间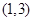 内,那么下面命题错误的( )
内,那么下面命题错误的( )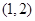 或
或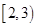 内有零点
内有零点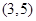 内无零点
内无零点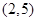 内有零点
内有零点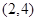 内不一定有零点
内不一定有零点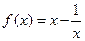
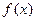 )在区间
)在区间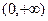 的单调性;
的单调性;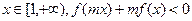 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。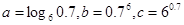 则( )
则( )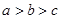
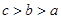
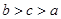
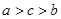
 的定义域是( )
的定义域是( )



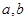 ,可按规则
,可按规则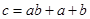 扩充为一个新数
扩充为一个新数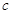 ,在
,在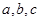 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.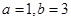 ,按上述规则操作三次,扩充所得的数是__________;
,按上述规则操作三次,扩充所得的数是__________;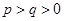 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为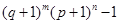 (
(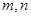 为正整数),则
为正整数),则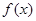 是定义在
是定义在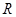 上的偶函数,且
上的偶函数,且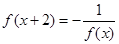 ,若当
,若当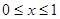 时,
时,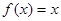 ,则
,则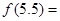 .
.  ,则满足
,则满足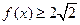 的
的 取值范围为__ ▲ ___
取值范围为__ ▲ ___