题目内容
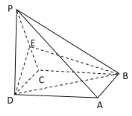
【题目】如图，在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA1＝2，E，E1分别是棱AD，AA1的中点．
（1）设F是棱AB的中点，证明：直线EE1∥平面FCC1；
（2）证明：平面D1AC⊥平面BB1C1C；
（3）求点D到平面D1AC的距离．
【答案】（1）详见解析（2）详见解析（3）
【解析】
试题分析：（1）要证直线EE1∥平面FCC1，只要证面C C1F∥面ADD1A1，根据面面平行的判定定理，结合平行四边形的性质证明；（2）根据面面垂直的判定定理，只要证明AC⊥面BCC1B1，再由线面垂直的判定定理只要证明AC垂直于BC、CC1；（3）利用等积法即VDD1AC＝VD1ADC，求出点D到平面D1AC的距离
试题解析：（1）
四边形
为平行四边形
又
面
,
面
面 2分
在直四棱柱中，
, 又面 ,面
面 3分
又
面
面//面
又
面,
面 5分
（2）
平行四边形是菱形
,易知
7分
在直四棱柱中，
面
,
面
又
面
9分
又
面
面
面 10分
（3）易知
11分
设
到面的距离为
，则
,又
14分
，即到面的距离为 ． 16分
【题目】某校为调查学生喜欢“应用统计”课程是否与性别有关，随机抽取了选修课程的55名学生，得到数据如下表：
喜欢统计课程 | 不喜欢统计课程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
（1）判断是否有99．5％的把握认为喜欢“应用统计”课程与性别有关？
（2）用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查，将这6名学生作为一个样本，从中任选2人，求恰有1个男生和1个女生的概率．
临界值参考:
| 0．10 | 0．05 | 0．25 | 0．010 | 0．005 | 0．001 |
| 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
（参考公式：
，其中
）
