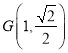题目内容
【题目】已知函数f(x)=x+ ![]() +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
【答案】
(1)证法一:∵函数f(x)=x+ ![]() +b,其中a,b是常数且a>0,
+b,其中a,b是常数且a>0,
任取设0<x1<x2≤ ![]() ,
,
则x1﹣x2<0,0<x1x2<a,
f(x1)﹣f(x2)=(x1+ ![]() +b)﹣(x2+
+b)﹣(x2+ ![]() +b)=(x1﹣x2)﹣
+b)=(x1﹣x2)﹣ ![]() =(x1﹣x2)
=(x1﹣x2) ![]() >0,
>0,
即f(x1)>f(x2),
∴f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
证法二:∵函数f(x)=x+ ![]() +b,其中a,b是常数且a>0,
+b,其中a,b是常数且a>0,
∴f′(x)=1﹣ ![]() =
= ![]() ,
,
当x∈(0, ![]() ]时,f′(x)≤0恒成立,
]时,f′(x)≤0恒成立,
故f(x)在区间(0, ![]() ]上是单调递减函数
]上是单调递减函数
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,
当a≤1时,即 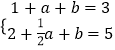 ,解得:a=﹣2(舍去);
,解得:a=﹣2(舍去);
当1<a≤2.25时,即 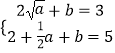 ,解得:a=0(舍去),或:a=16(舍去);
,解得:a=0(舍去),或:a=16(舍去);
当2.25<a<4时, ![]() ,解得:a=3+2
,解得:a=3+2 ![]() (舍去),
(舍去),
当a≥4时,即 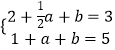 ,解得:a=6;
,解得:a=6;
综上可得:a=6
【解析】(1)证法一:任取设0<x1<x2≤ ![]() ,作差比较可得f(x1)>f(x2),结合函数单调性的定义,可得:f(x)在区间(0,
,作差比较可得f(x1)>f(x2),结合函数单调性的定义,可得:f(x)在区间(0, ![]() ]上是单调递减函数;证法二:求导,分析出当x∈(0,
]上是单调递减函数;证法二:求导,分析出当x∈(0, ![]() ]时,f′(x)≤0恒成立,故f(x)在区间(0,
]时,f′(x)≤0恒成立,故f(x)在区间(0, ![]() ]上是单调递减函数;(2)结合对勾函数的图象和性质,分析函数f(x)在区间[1,2]上f(x)的最值,可求出满足条件的a值.
]上是单调递减函数;(2)结合对勾函数的图象和性质,分析函数f(x)在区间[1,2]上f(x)的最值,可求出满足条件的a值.
【考点精析】掌握函数单调性的判断方法和函数的最值及其几何意义是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x/span>1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

 英才计划期末调研系列答案
英才计划期末调研系列答案