题目内容
设各项均为正数的数列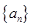 的前
的前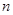 项和为
项和为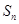 ,满足
,满足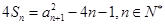 ,且
,且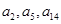 恰为等比数列
恰为等比数列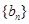 的前三项.
的前三项.
(1)证明:数列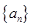 为等差数列; (2)求数列
为等差数列; (2)求数列 的前
的前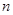 项和
项和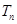 .
.
(1)见解析; (2)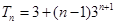 .
.
解析试题分析:(1)根据递推关系式得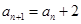 ,结合
,结合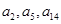 恰为等比数列
恰为等比数列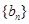 的前三项,得到结论. (2)先由
的前三项,得到结论. (2)先由 得到
得到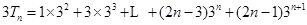 ,两式相减,利用错位相减法求前n项和. 所以
,两式相减,利用错位相减法求前n项和. 所以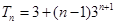 .
.
(1)当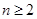 时,
时,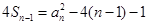 ,则
,则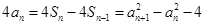 ,
,
于是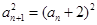 ,而,
,而,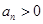 ,故
,故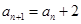 , 2分
, 2分
所以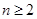 时,
时,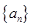 为公差为2的等差数列,
为公差为2的等差数列,
因为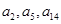 恰为等比数列
恰为等比数列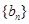 的前三项,所以
的前三项,所以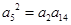
即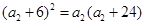 ,解得
,解得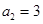 , 3分
, 3分
由条件知 ,则
,则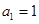 , 4分
, 4分
于是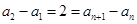 ,
,
所以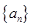 为首项是1,公差为2的等差数列; 6分
为首项是1,公差为2的等差数列; 6分
(2)由(1)知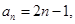
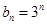 , 8分
, 8分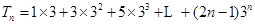 ,
,
两边同乘以3得,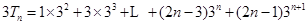 , 9分
, 9分
两式相减得
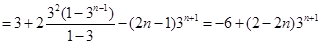 , 12分
, 12分
所以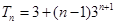 . 13分
. 13分
考点:递推关系式;等差数列的通项公式;错位相减法.

练习册系列答案
相关题目
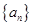 中,
中,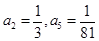
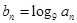 ,求数列
,求数列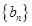 的前n项和
的前n项和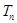 .
.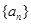 的前n项和为
的前n项和为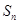 ,已知
,已知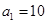 ,
,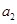 为整数,且
为整数,且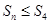 .
.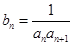 ,求数列
,求数列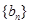 的前n项和
的前n项和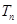 .
. 的前
的前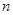 项和为
项和为 ,
,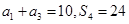 .
.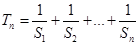 ,求
,求 .
. 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
 为
为 阶“期待数列”:
阶“期待数列”: ,②
,② .
. 为
为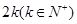 阶“期待数列”,求公比
阶“期待数列”,求公比 ;
; 阶“期待数列”
阶“期待数列” 的前
的前 项和为
项和为 .
. )求证:
)求证: ;
;
 ,使
,使 ,试问数列
,试问数列
 是否为
是否为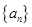 的首项
的首项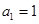 ,公差
,公差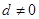 ,等比数列
,等比数列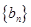 满足
满足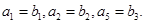
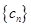 对任意
对任意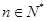 均有
均有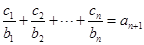 ,求数列
,求数列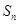 .
. 的前
的前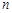 项和
项和 ,数列
,数列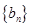 满足
满足 .
.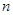 项和
项和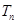 .
. 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列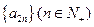 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 项和为
项和为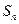 .
. ;
;