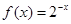题目内容
已知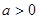 ,函数
,函数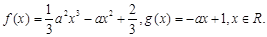
(1)当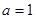 时,求函数
时,求函数 在点(1,
在点(1,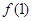 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在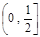 上至少存在一个实数x0,使
上至少存在一个实数x0,使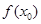 >g(xo)成立,求正实数
>g(xo)成立,求正实数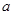 的取值范围。
的取值范围。
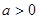 ,函数
,函数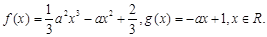
(1)当
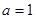 时,求函数
时,求函数 在点(1,
在点(1,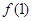 )的切线方程;
)的切线方程;(2)求函数
 在[-1,1]的极值;
在[-1,1]的极值;(3)若在
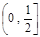 上至少存在一个实数x0,使
上至少存在一个实数x0,使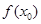 >g(xo)成立,求正实数
>g(xo)成立,求正实数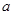 的取值范围。
的取值范围。(Ⅰ) 函数 在点(1,
在点(1,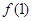 )的切线方程为
)的切线方程为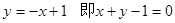
(Ⅱ)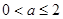 时,极大值为
时,极大值为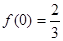 ,无极小值
,无极小值
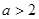 时 极大值是
时 极大值是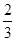 ,极小值是
,极小值是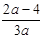
(Ⅲ)(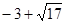
 ,
,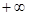 )
)
 在点(1,
在点(1,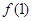 )的切线方程为
)的切线方程为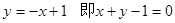
(Ⅱ)
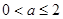 时,极大值为
时,极大值为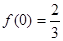 ,无极小值
,无极小值 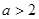 时 极大值是
时 极大值是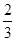 ,极小值是
,极小值是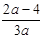
(Ⅲ)(
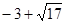
 ,
,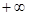 )
)本试题中导数在研究函数中的运用。(1)中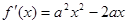 ,那么当
,那么当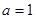 时,
时,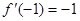 又
又 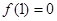 所以函数
所以函数 在点(1,
在点(1,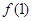 )的切线方程为
)的切线方程为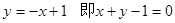 ;(2)中令
;(2)中令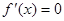 有
有 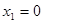
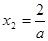
对a分类讨论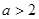 ,和
,和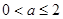 得到极值。(3)中,设
得到极值。(3)中,设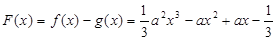 ,
,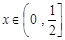 ,依题意,只需
,依题意,只需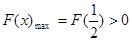 那么可以解得。
那么可以解得。
解:(Ⅰ)∵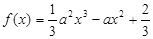 ∴
∴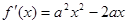
∴ 当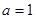 时,
时,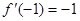 又
又 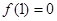
∴ 函数 在点(1,
在点(1,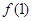 )的切线方程为
)的切线方程为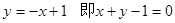 --------4分
--------4分
(Ⅱ)令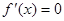 有
有 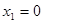
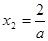
① 当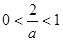 即
即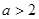 时
时
故 的极大值是
的极大值是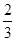 ,极小值是
,极小值是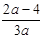
② 当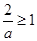 即
即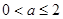 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为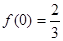 ,无极小值。
,无极小值。
综上所述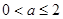 时,极大值为
时,极大值为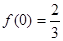 ,无极小值
,无极小值
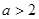 时 极大值是
时 极大值是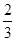 ,极小值是
,极小值是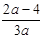 ----------8分
----------8分
(Ⅲ)设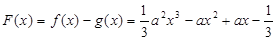 ,
,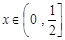
对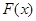 求导,得
求导,得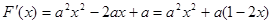
∵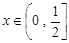 ,
,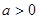
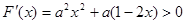
∴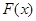 在区间
在区间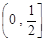 上为增函数,则
上为增函数,则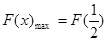
依题意,只需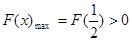 ,即
,即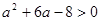
解得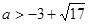 或
或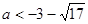 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(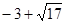
 ,
,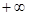 )
)
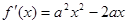 ,那么当
,那么当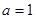 时,
时,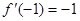 又
又 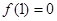 所以函数
所以函数 在点(1,
在点(1,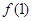 )的切线方程为
)的切线方程为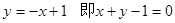 ;(2)中令
;(2)中令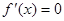 有
有 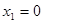
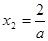
对a分类讨论
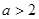 ,和
,和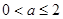 得到极值。(3)中,设
得到极值。(3)中,设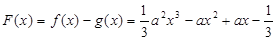 ,
,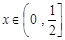 ,依题意,只需
,依题意,只需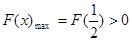 那么可以解得。
那么可以解得。解:(Ⅰ)∵
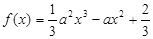 ∴
∴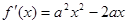
∴ 当
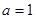 时,
时,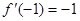 又
又 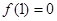
∴ 函数
 在点(1,
在点(1,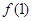 )的切线方程为
)的切线方程为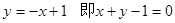 --------4分
--------4分(Ⅱ)令
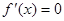 有
有 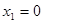
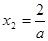
① 当
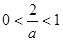 即
即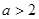 时
时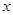 | (-1,0) | 0 | (0,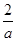 ) ) | 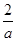 | (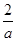 ,1) ,1) |
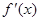 | + | 0 | - | 0 | + |
 |  | 极大值 |  | 极小值 |  |
 的极大值是
的极大值是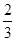 ,极小值是
,极小值是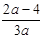
② 当
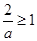 即
即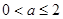 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为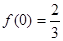 ,无极小值。
,无极小值。 综上所述
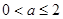 时,极大值为
时,极大值为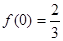 ,无极小值
,无极小值 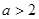 时 极大值是
时 极大值是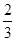 ,极小值是
,极小值是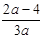 ----------8分
----------8分(Ⅲ)设
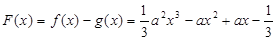 ,
,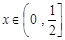
对
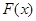 求导,得
求导,得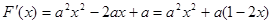
∵
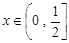 ,
,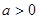
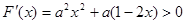
∴
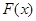 在区间
在区间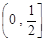 上为增函数,则
上为增函数,则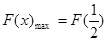
依题意,只需
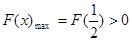 ,即
,即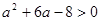
解得
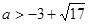 或
或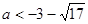 (舍去)
(舍去)则正实数
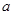 的取值范围是(
的取值范围是(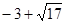
 ,
,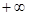 )
)
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
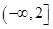 ,
,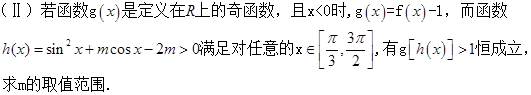
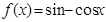 ;②
;②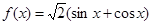 ;③
;③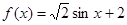 ;④
;④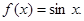 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )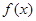 对任意
对任意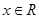 都有
都有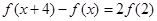 ,若
,若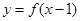 的图象关于直线
的图象关于直线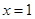 对称,且
对称,且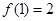 ,则
,则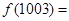 ( )
( )  随自变量
随自变量 变化的一组数据,由此可判断它最可能的函数模型为
变化的一组数据,由此可判断它最可能的函数模型为



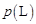 关于行驶速度
关于行驶速度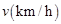 的函数解析式可以表示为:
的函数解析式可以表示为: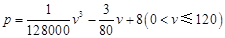 .已知甲、乙两地相距
.已知甲、乙两地相距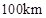 ,设汽车的行驶速度为
,设汽车的行驶速度为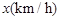 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为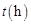 ,耗油量为
,耗油量为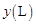 .
.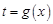 及
及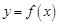 ;
;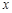 为多少时,
为多少时,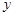 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值. ,则函数
,则函数 的解析式
的解析式 .
. 是奇函数,且
是奇函数,且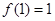 .若
.若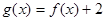 ,则
,则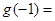 .
. 满足
满足 ,则
,则