题目内容
已知f(x)是定义在(-2,2)上的偶函数,且在[0,2)上单调递减,若f(1-a)<f(a),求实数a的取值范围.
答案:
解析:
解析:
|
解:f(x)是定义在(-2,2)上的偶函数, 则f(1-a)<f(a)可等价为f(|1-a|)<f(|a|),且1-a与a均在(-2,2)内. 由f(x)在[0,2)上单调递减,知|1-a|>|a|. 因此 故a的取值范围是 点评:本题易忽视复合函数的定义域,从而得错解.在解题中利用偶函数避免了分类讨论. |

练习册系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 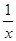 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
