题目内容
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R,满足f(a·b)=af(b)+bf(a),f(2)=2,a![]() =
=![]() (n∈N*),b
(n∈N*),b![]() =
=![]() (n∈N*);考查下列结论:
(n∈N*);考查下列结论:
①f(0)=f(1);②f(x)为偶函数;③数列{a![]() }为等比数列;④{b
}为等比数列;④{b![]() }为等差数列.
}为等差数列.
其中正确的是 .
①③④
解析:
将数列的前几项写出f (2)=1×2;f (2![]() )=2×2
)=2×2![]() ;f (2
;f (2![]() )=3×2
)=3×2![]() ;f (2
;f (2![]() )=4×2
)=4×2![]() ,…,归纳猜想得:f (2
,…,归纳猜想得:f (2![]() )=n×2
)=n×2![]() ,从而a
,从而a![]() =2
=2![]() ,b
,b![]() =n.由已知f (a·b)=af (b)+bf (a),得f (0×0)=0×f (0)+0×f (0)=0,f (1×1)=1×f (1)+1×f (1)
=n.由已知f (a·b)=af (b)+bf (a),得f (0×0)=0×f (0)+0×f (0)=0,f (1×1)=1×f (1)+1×f (1)![]() f (1)=0.故f (0)=f (1),若取a=b=x时,得2xf (x)=f (x
f (1)=0.故f (0)=f (1),若取a=b=x时,得2xf (x)=f (x![]() ),即f (x)=
),即f (x)=![]() ;若取a=b=-x时,得-2xf (-x)=f (x
;若取a=b=-x时,得-2xf (-x)=f (x![]() ),即f (-x)=-
),即f (-x)=-![]() ,故该函数为奇函数,所以①③④正确.
,故该函数为奇函数,所以①③④正确.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 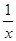 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
