Question

【题目】已知函数 ，则函数y=f（x）的大致图象为（　　）
A.
B.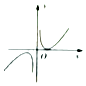
C.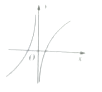
D.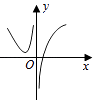

Answer 1

【答案】D
【解析】解：由题意可得函数的定义域为（﹣∞，0）∪（0，+∞），

函数 ，可得f（﹣x）≠±f（x），

故函数为非奇非偶函数，排除：B、C；

当x＞0时，函数 =x2﹣ ，f′（x）=2x﹣ = ，

令g（x）=x3+1﹣lnx，（x＞0），

g′（x）=3x2﹣ = ，

令g′（x）=0，解得x= ，

故当0＜x＜ 时，g′（x）＜0，g（x）是减函数，

x＞ 时，函数g（x）是单调递增，g（x）的最小值为g（ ）= ＞0，

∴f′（x）＞0在x＞0时，恒成立，函数是单调增函数，排除A；

综上可得选项D符合题意，

故答案为：D．

根据函数的解析式，得出函数的定义域，先判断出函数非奇非偶，图象即不关于原点对称也不关于y轴对称，再对函数求导，找到函数的单调区间即可判断出函数图象.