题目内容
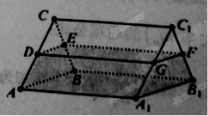
【题目】如图所示,在四棱锥![]() 中,底面四边形
中,底面四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 中点,
中点,![]() 平面
平面![]() ,
,![]() .
.
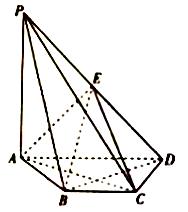
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为30°,求二面角
所成的角为30°,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明面面垂直,实质为证明线面垂直,而线面垂直的证明,往往从两个方面进行,一是结合平几知识寻找线线垂直,本题直角给出![]() 另一方面,结合立几中线面垂直条件
另一方面,结合立几中线面垂直条件![]() 平面
平面![]() 得线线垂直
得线线垂直![]() (2)涉及二面角问题,一般利用空间向量进行解决,首先根据题意建立恰当的空间直角坐标系,设立各点坐标,利用方程组求各面的法向量,结合向量数量积求向量夹角,最后根据二面角与向量夹角的关系,求出二面角的余弦值
(2)涉及二面角问题,一般利用空间向量进行解决,首先根据题意建立恰当的空间直角坐标系,设立各点坐标,利用方程组求各面的法向量,结合向量数量积求向量夹角,最后根据二面角与向量夹角的关系,求出二面角的余弦值
试题解析:(1)因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,.
,.
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)设![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
由(1)知,![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,从而
所成的角,从而![]() ,
,
在![]() 中,由
中,由![]() ,得
,得![]() ,
,
因为四边形![]() 为等腰梯形,
为等腰梯形,![]() ,
,
所以![]() 均为等腰直角三角形,所以
均为等腰直角三角形,所以![]() ,
,
所以![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则
![]()
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() 得
得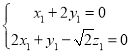 ,
,
令![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() 得
得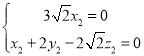 ,
,
令![]() ,得
,得![]() ,
,
所以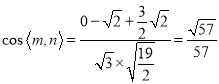 ,
,
因为二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】四个小动物换座位,开始时鼠、猴、兔、猫分别坐1,2,3,4号座位上(如图).第1次前后排动物互换座位,第2次左右列动物互换座位……这样交替进行下去,那么第2 005次互换座位后,小兔的座位号是( )
1鼠 | 2猴 |
3兔 | 4猫 |
开始
1兔 | 2猫 |
3鼠 | 4猴 |
第一次
1猫 | 2兔 |
3猴 | 4鼠 |
第二次
1猴 | 2鼠 |
3猫 | 4兔 |
第三次
A. 1 B. 2 C. 3 D. 4