题目内容
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由已知条件可推得![]() ,由此能求出椭圆的标准方程;(2)存在直线
,由此能求出椭圆的标准方程;(2)存在直线![]() 使得
使得![]() 成立,直线方程与椭圆的方程联立,由此利用根的判别式和韦达定理结合已知条件,得出
成立,直线方程与椭圆的方程联立,由此利用根的判别式和韦达定理结合已知条件,得出![]() ,即可求解实数
,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]() (
(![]() ),半焦距为
),半焦距为![]() .依题意
.依题意![]() ,由右焦点到右顶点的距离为
,由右焦点到右顶点的距离为![]() ,得
,得![]() .解得
.解得![]() ,
,![]() .所以
.所以![]() .
.
所以椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)解:存在直线![]() ,使得
,使得![]() 成立.理由如下:
成立.理由如下:
由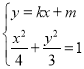 得
得![]() .
.
![]() ,化简得
,化简得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
若![]() 成立,即
成立,即![]() ,等价于
,等价于![]() .
.
所以![]() .
.![]() ,
,
![]() ,
,![]() ,
,
化简得,![]() .将
.将![]() 代入
代入![]() 中,
中,![]() ,解得,
,解得, ![]() .又由
.又由![]() ,
,![]() ,
,
从而![]() ,
,![]() 或
或![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据如下:

![]()