题目内容
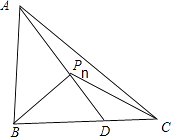
【题目】已知数列{an}中，a1=2，点列Pn（n=1，2，…）在△ABC内部，且△PnAB与△PnAC的面积比为2：1，若对n∈N*都存在数列{bn}满足 
，则a4的值为 ．
【答案】80
【解析】解：在BC上取点D，使得BD=2CD，则Pn在线段AD上．
∵ 
，
∴﹣ 
an+1 
=bn 
+（3an+2） 
=bn（ ﹣ 
）+（3an+2）（ ﹣ 
），
∴（﹣ an+1﹣bn﹣3an﹣2） =﹣bn ﹣（3an+2） =﹣bn ﹣ 
（3an+2） 
，
∵A，Pn，D三点共线，
∴﹣ an+1﹣bn﹣3an﹣2=﹣bn﹣ （3an+2），即an+1=3an+2．
∴a2=3a1+2=8，
a3=3a2+2=26，
a4=3a3+2=80．
所以答案是：80．
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识，掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
