题目内容
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.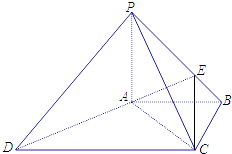
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
【答案】
(1)解:∵PA⊥底面ABCD,BC底面ABCD,∴PA⊥BC,
又∵AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.
∵BC平面PCB,∴平面PAB⊥平面PCB.
(2)∵PA⊥底面ABCD,∴AC为PC在平面ABCD内的射影.
又∵PC⊥AD,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得 ![]() ,
,
∴ ![]() .
.
又∵AC⊥AD,故△DAC为等腰直角三角形.
∴ ![]() .
.
连接BD,交AC于点M,则由AB∥CD得: ![]() .
.
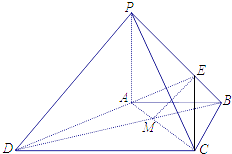
在△BPD中, ![]() ,所以PD∥EM
,所以PD∥EM
又∵PD平面EAC,EM平面EAC,
∴PD∥平面EAC.
【解析】1、由线面垂直得到线线垂直,再由线线垂直得到线面垂直,根据线线垂直的判定定理可得证。
2、做辅助线连接BD,交AC于点M,连接EM由射影定理可得AC⊥AD. 在梯形ABCD中,由AB⊥BC,AB=BC,得 ∠ D C A = ∠ B A C = ![]() ,∵AC⊥AD,故△DAC为等腰直角三角形. D C =
,∵AC⊥AD,故△DAC为等腰直角三角形. D C = ![]() A C =
A C = ![]() (
( ![]() A B ) = 2 A B ,由AB∥CD得
A B ) = 2 A B ,由AB∥CD得 ![]() ,在△BPD中,
,在△BPD中, ![]() ,所以PD∥EM,又∵PD平面EAC,EM平面EAC,∴PD∥平面EAC.
,所以PD∥EM,又∵PD平面EAC,EM平面EAC,∴PD∥平面EAC.

练习册系列答案
相关题目