题目内容
【题目】设命题p:对任意的 ![]() ,sinx≤ax+b≤tanx恒成立,其中a,b∈R.
,sinx≤ax+b≤tanx恒成立,其中a,b∈R.
(1)若a=1,b=0,求证:命题p为真命题.
(2)若命题p为真命题,求a,b的所有值.
【答案】
(1)证明:若a=1,b=0,则命题p:对任意的 ![]() ,sinx≤x≤tanx恒成立,
,sinx≤x≤tanx恒成立,
如图由三角函数线的定义可知,
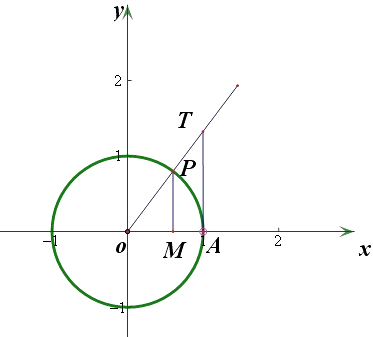
sinx=MP,cosx=OM,x= ![]() ,
,
tanx=AT.
∵ ![]() 时
时
S△AOP= ![]() |OA||MP|=
|OA||MP|= ![]() sinx,
sinx,
S扇形AOP= ![]() |OA|=
|OA|= ![]() x,
x,
S△AOT= ![]() |OA||AT|=
|OA||AT|= ![]() tanx,
tanx,
且S△AOP<S扇形AOP<SAOT.
∴ ![]() sinx<
sinx< ![]() x<
x< ![]() tanx
tanx
即sinx<x<tanx
(2)证明:若命题p为真命题,则当x=0时,sin0≤b≤tan0,所以b=0,
此时sinx≤ax≤tanx恒成立,
若a<1,令f(x)=ax﹣sinx, ![]() ,
,
则f′(x)=a﹣cosx=0在 ![]() 时有唯一解,记为x0,
时有唯一解,记为x0,
当x∈[0,x0)时,f′(x)<0,
此时f(x)≤f(0)=0恒成立,即ax≤sinx,矛盾,舍去;
若a>1,令h(x)=ax﹣tanx, ![]() ,
,
则h′(x)=a﹣ ![]() =0在
=0在 ![]() 时有唯一解,记为x1,
时有唯一解,记为x1,
当x∈[0,x1)时,h′(x)>0,
此时h(x)≥h(0)=0恒成立,即ax≥tanx,矛盾,舍去;
故a=1,b=0.
【解析】(1)在直角坐标系中,以坐标原点为圆心画一个单位圆,与x轴正半轴交于点A,在第一象限内的圆周上任取一点P,过点P作x轴的垂线,垂足为M,过点A作x轴的垂线,交射线OP于点T,根据三角函数线可知sinx=MP,tanx=AT,那么S![]() AOP=
AOP=![]() sinx,S扇形AOP=
sinx,S扇形AOP=![]() x,S
x,S![]() AOT=
AOT=![]() tanx,通过比较S
tanx,通过比较S![]() AOP、S扇形AOP、S
AOP、S扇形AOP、S![]() AOT即可;(2)当x=0时,b=0,;根据a分类讨论:当a
AOT即可;(2)当x=0时,b=0,;根据a分类讨论:当a![]() 1时构造函数f(x)=ax-sinx,当a
1时构造函数f(x)=ax-sinx,当a![]() 1时构造函数f(x)=ax-tanx,利用导数分别讨论两个函数的单调性.
1时构造函数f(x)=ax-tanx,利用导数分别讨论两个函数的单调性.
【考点精析】本题主要考查了命题的真假判断与应用和利用导数研究函数的单调性的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案