题目内容
【题目】如图,在三棱锥A﹣BOC中,OA,OB,OC两两垂直,点D,E分别为棱BC,AC的中点,F在棱AO上,且满足OF= ![]() ,已知OA=OC=4,OB=2.
,已知OA=OC=4,OB=2.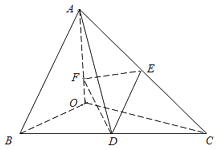
(1)求异面直线AD与OC所成角的余弦值;
(2)求二面角C﹣EF﹣D的正弦值.
【答案】
(1)解:如图,以O为原点,分别以OB、OC、OA所在直线为x轴、y轴、z轴正方向建立空间直角坐标系.

依题意可得:O(0,0,0),A(0,0,4),B(2,0,0),C(0,4,0),D(1,2,0),E(0,2,2),F(0,0,1),
∴ ![]() ,
, ![]() ,
,
于是 ![]() ,
, ![]() ,
, ![]() ,
,
∴cos< ![]() >=
>= 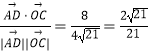
(2)解:平面AOC的一个法向量为 ![]() .
.
设 ![]() 为平面DEF的一个法向量,
为平面DEF的一个法向量,
又 ![]() ,
, ![]() ,
,
则 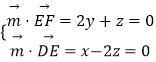 ,取z=2,则x=4,y=﹣1,
,取z=2,则x=4,y=﹣1,
∴ ![]() 为平面DEF的一个法向量,
为平面DEF的一个法向量,
从而cos< ![]() >=
>= 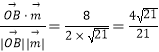 ,
,
设二面角C﹣EF﹣D的大小为θ,则|cosθ|= ![]() .
.
∵θ∈[0,π],∴sinθ= ![]() .
.
因此二面角C﹣EF﹣D的正弦值为 ![]() .
.
【解析】(1)根据题意建立空间直角坐标系,进而求出各个点的坐标,进而得到![]() 和
和![]() 的坐标,利用向量的数量积公式可求出其余弦值。(2)根据题意可得平面AOC的一个法向量为
的坐标,利用向量的数量积公式可求出其余弦值。(2)根据题意可得平面AOC的一个法向量为 ![]() = ( 2 , 0 , 0 ) .求出平面DEF的一个法向量
= ( 2 , 0 , 0 ) .求出平面DEF的一个法向量![]() 的坐标,利用向量的数量积可求出二面角平面角的余弦值,进而得到正弦值。
的坐标,利用向量的数量积可求出二面角平面角的余弦值,进而得到正弦值。
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
相关题目