题目内容
【题目】设函数f（x）=1﹣ 
（x∈R），
（1）求反函数f﹣1（x）；
（2）解不等式f﹣1（x）＞log2（1+x）+1．
【答案】
（1）解：∵函数y=f（x）=1﹣ 
（x∈R），
∴ =1﹣y，
∴2x= 
，
∴x=log2 ，且﹣1＜y＜1；
∴f（x）的反函数是y=f﹣1（x）=log2 
，x∈（﹣1，1）
（2）解：不等式f﹣1（x）＞log2（1+x）+1可化为
log2 ＞log22（1+x），
等价于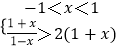 
，
解得 
＜x＜1，
∴该不等式的解集为（ ，1）
【解析】（1）令y=f（x），用y表示出x即可得出f（x）的反函数是y=f﹣1（x）；（2）把不等式f﹣1（x）＞log2（1+x）+1转化为log2 ＞log22（1+x），写出等价的不等式组，求解集即可．
练习册系列答案
相关题目
