题目内容
用数学归纳法证明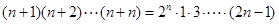 ,从k到k+1,左边需要增乘的代数式为________
,从k到k+1,左边需要增乘的代数式为________
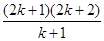 (2(2k+1)也可)
(2(2k+1)也可)
解析试题分析:当n=k时,左边等于 (k+1)(k+2)…(k+k)=(k+1)(k+2)…(2k),
当n=k+1时,左边等于 (k+2)(k+3)…(k+k)(2k+1)(2k+2),
故从“k”到“k+1”的证明,左边需增添的代数式是 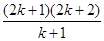 =2(2k+1),
=2(2k+1),
故答案为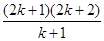 或 2(2k+1)。
或 2(2k+1)。
考点:本题主要考查用数学归纳法证明等式的方法步骤。
点评:简单题,注意分析从“k”到“k+1”的变化规律,用n=k+1时左边的式子,除以n=k时左边的式子,即得所求。

练习册系列答案
相关题目
 cr、
cr、 ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________. ,
, ,
, ,……
,…… ,则按此规律可猜想第n个不等式为 .
,则按此规律可猜想第n个不等式为 . ,
, ,
, ,…,
,…, ,
, ,
, ,
, , ,则可以归纳出第
, ,则可以归纳出第 个式子为
个式子为 
 ,
,
 的自然数
的自然数 的
的 次方幂有如下分解方式:
次方幂有如下分解方式:





 , 若
, 若 的分解中最小的数是73,则
的分解中最小的数是73,则 ;②
;② ;③
;③ ;…………… 照此规律,第五个不等式为 .
;…………… 照此规律,第五个不等式为 .