题目内容
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为 cr、
cr、 ar、
ar、 br,由S=
br,由S= cr+
cr+ ar+
ar+ br得r=
br得r= ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
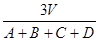
解析试题分析:根据类比推理的意义,类比推理是根据两个或两类对象有部分属性相同,从而推出它们的其他属性也相同的推理。对照三角形OAB、OBC、OAC的面积分别为 cr、
cr、 ar、
ar、 br,由S=
br,由S= cr+
cr+ ar+
ar+ br得r=
br得r= ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=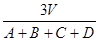 。
。
考点:类比推理
点评:简单题,类比推理是以关于两个事物某些属性相同的判断为前提,推出两个事物的其他属性相同的结论的推理。一般的,点对线,距离对面积,面积对体积等。

练习册系列答案
相关题目
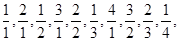 …,依它的10项的规律,则a99+a100的值为______.
…,依它的10项的规律,则a99+a100的值为______. , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: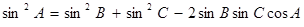
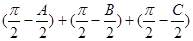 =
= 分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以 则:若锐角A, B, C满
则:若锐角A, B, C满 ,
, .
. _____.
_____. 表示不超过
表示不超过 的最大整数.
的最大整数. 
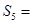 .
.  ,观察:
,观察:



 且
且 时,
时, .
.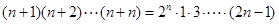 ,从k到k+1,左边需要增乘的代数式为________
,从k到k+1,左边需要增乘的代数式为________