题目内容
18.已知函数y=f(x)满足对于任意的x>0恒有f(3x)=3f(x)成立,当1≤x≤3时,f(x)=1-|x-2|,则集合{x|f(x)=f(33)}中最小的元素为15.分析 根据条件求出f(33)的值,根据条件关系,将函数转化为分段函数形式,进行解方程即可.
解答 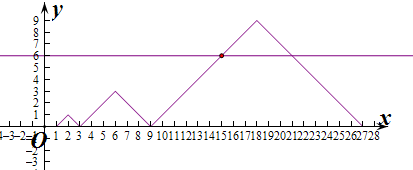 解:由题意:
解:由题意:
f(33)=3f(11)=9f($\frac{11}{3}$)=27f($\frac{11}{9}$),
又∵$\frac{11}{9}$∈[1,3],∴f($\frac{11}{9}$)=1-|$\frac{11}{9}$-2|=$\frac{2}{9}$
∴f(33)=27f($\frac{11}{9}$)=27×$\frac{2}{9}$=6;
∵x∈[1,3]有f(x)=1-|x-2|=$\left\{\begin{array}{l}{x-1,}&{1≤x<2}\\{3-x,}&{2≤x≤3}\end{array}\right.$,
∴若x∈[3,9],则$\frac{x}{3}$∈[1,3],f(x)=f(3•$\frac{x}{3}$)=3f($\frac{x}{3}$)=3[1-|$\frac{x}{3}$-2|],
若x∈[9,27],则$\frac{x}{3}$∈[3,9],f(x)=f(3•$\frac{x}{3}$)=3f($\frac{x}{3}$)=9[1-|$\frac{x}{9}$-2|],
作出函数在[1,27]上的图象如图:
若f(x)=f(33)=6,
则满足条件的最小x∈[9,18],
此时有9[1-|$\frac{x}{9}$-2|]=6,
得|$\frac{x}{9}$-2|=$\frac{1}{3}$,
解得x=15,
故最小的元素为15,
故答案为:15.
点评 本题考查函数的性质,方程解的求解,根据条件将函数转化为分段函数形式是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
13.若(2x-1)2015=a0+a1x+a2x2+…+a2015x2015(x∈R),则$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2015}}}}{{{2^{2015}}{a_1}}}$的值为( )
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | $\frac{1}{4030}$ | D. | -$\frac{1}{4030}$ |
3.若集合A={x|2${\;}^{{x}^{2}-4x-5}$>1},集合B={x|y=lg$\frac{2-x}{2+x}$},则A∩B=( )
| A. | {x|-5<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<-1} | D. | {x|-5<x<-1} |