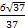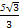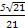题目内容
已知双曲线的中心在原点,一个焦点为F1(- ,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )
,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )
A. -y2=1 -y2=1 | B.x2- =1 =1 |
C.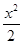 - - =1 =1 | D.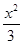 - - =1 =1 |
B
解析

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
过椭圆 右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
右焦点且斜率为1的直线被椭圆截得的弦MN的长为( )
A. | B. | C. | D. |
如图所示,已知A,B分别为椭圆 +
+ =1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
A.± | B.± |
C.± | D.± |
已知双曲线 -
- =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.y=± x x | B.y=± x x |
| C.y=±2x | D.y=± x x |
O为坐标原点,F为抛物线C:y2=4 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4 ,则△POF的面积为( )
,则△POF的面积为( )
| A.2 | B.2 | C.2 | D.4 |
已知F是抛物线y2=4x的焦点,P是圆x2+y2-8x-8y+31=0上的动点,则|FP|的最小值是( )
| A.3 | B.4 | C.5 | D.6 |
 ,
, 是椭圆长轴的一个端点,
是椭圆长轴的一个端点, 是椭圆短轴的一个端点,
是椭圆短轴的一个端点, 为椭圆的一个焦点.若
为椭圆的一个焦点.若 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )



 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线 上的点
上的点 ,经直线反射后又回到点
,经直线反射后又回到点 ,则
,则 等于( )
等于( )




 -
-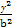 =1(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线x=
=1(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线x= y2的焦点分成3∶2的两段,则此双曲线的离心率为( )
y2的焦点分成3∶2的两段,则此双曲线的离心率为( )