题目内容
(本小题满分14分)已知函数 =
=
(1) 若 存在单调增区间,求
存在单调增区间,求 的取值范围;
的取值范围;
(2)是否存在实数 >0,使得方程
>0,使得方程 在区间
在区间 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出 的取值范围?若不存在,请说明理由.
的取值范围?若不存在,请说明理由.
(1)a的取值范围是(-1, 0)∪(0, +∞)
(2) , 所以a的取值范围是(1,
, 所以a的取值范围是(1,  )
)
【解析】答:(1)由已知,得h(x)=  且x>0, …………………...1f
且x>0, …………………...1f
则hˊ(x)=ax+2- =
= ,…………………………………………………2f
,…………………………………………………2f
∵函数h(x)存在单调递增区间,
∴hˊ(x)>0有解, 且解满足 ……………………….……3f
……………………….……3f
即不等式ax2+2x-1>0有满足 ……………………..……4f
……………………..……4f
当a<0时, y=ax2+2x-1的图象为开口向下的抛物线, 要使ax2+2x-1≥0总有x>0的解, 则方程ax2+2x-1=0至少有一个不重复正根, 而方程ax2+2x-1=0总有两个不相等的根时, 则必定是两个不相等的正根. 故只需Δ=4+4a>0, 即a>-1. 即-1<a<0……………….5f
当a>0 时, y= ax2+2x-1的图象为开口向上的抛物线, ax2+2x-1≥0 一定有x>0的解. …………………………………………………………………………….……...6f
综上, a的取值范围是(-1, 0)∪(0, +∞) ……………………………………….……. 7f
解法二、同解法一…….
即不等式ax2+2x-1>0有满足 ……………………….……4f
……………………….……4f
即 有解……………………………………………………….5f
有解……………………………………………………….5f
令 的最小值为
的最小值为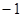 ……………………………………..……6f
……………………………………..……6f
结合题设得a的取值范围是(-1, 0)∪(0, +∞) ……………………………………… 7f
解法三、同解法一……….
即不等式ax2+2x-1>0有满足 ……………………..……4f
……………………..……4f
(1)当 ,
,  ,ax2+2x-1>0没有符合条解………………………5f
,ax2+2x-1>0没有符合条解………………………5f
(2)当 ,方程
,方程 的两根是
的两根是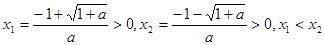 ,此时,区间
,此时,区间 是所求的增区间。.
是所求的增区间。.
………………………………………………………………………………………………6f
当 ,方程
,方程 的两根是,
的两根是,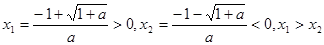 ,区间
,区间 为所求的增区
为所求的增区
综上, a的取值范围是(-1, 0)∪(0, +∞) ……………………………………….……. 7f
(2)解法一、方程
即为
等价于方程ax2+(1-2a)x-lnx=0 . ………………………………………………….. 8f
设H(x)= ax2+(1-2a)x-lnx, 于是原方程在区间( )内根的问题, 转化为函数H(x)在区间(
)内根的问题, 转化为函数H(x)在区间( )内的零点问题………………………………………………………………….... 9f
)内的零点问题………………………………………………………………….... 9f
Hˊ(x)=2ax+(1-2a)- =
= ……….….….10f
……….….….10f
当x∈(0, 1)时, Hˊ(x)<0, H(x)是减函数; 当x∈(1, +∞)时, Hˊ(x)>0, H(x)是增函数;
若H(x)在( )内有且只有两个不相等的零点, 只须
)内有且只有两个不相等的零点, 只须
 ……………..…13f
……………..…13f
解得 , 所以a的取值范围是(1,
, 所以a的取值范围是(1,  ) …………………… …..14f
) …………………… …..14f

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)