题目内容
从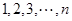 中这
中这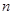 个数中取
个数中取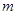 (
(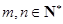 ,
,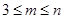 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为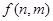 .
.
(1)当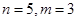 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及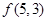 的值;
的值;
(2)求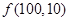 ;
;
(3)求证: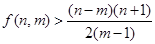 .
.
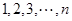 中这
中这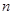 个数中取
个数中取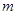 (
(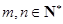 ,
,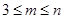 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为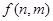 .
.(1)当
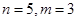 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及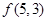 的值;
的值;(2)求
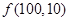 ;
;(3)求证:
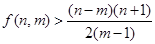 .
.(1)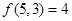 ;(2)
;(2)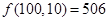 ;(3)详见解析.
;(3)详见解析.
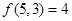 ;(2)
;(2)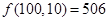 ;(3)详见解析.
;(3)详见解析.试题分析:(1)符合要求的递增等差数列全部列出,即可求出
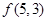 的值;(2)求
的值;(2)求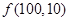 ,即从
,即从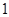 到
到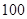 个数中取
个数中取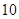 个,组成递增等差数列,由等差数列的性质知
个,组成递增等差数列,由等差数列的性质知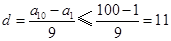 ,故分别取
,故分别取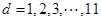 ,讨论各种情况下,数列的个数,如
,讨论各种情况下,数列的个数,如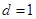 时,
时,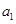 分别取
分别取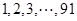 ,共可得
,共可得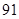 个符合要求的数列,以此类推,即可得到其他情况的符合要求的数列的个数,加起来的和即为符合要求数列的个数,即得
个符合要求的数列,以此类推,即可得到其他情况的符合要求的数列的个数,加起来的和即为符合要求数列的个数,即得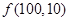 的值;(3)求证:
的值;(3)求证: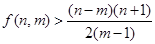 ,由(2)的求解过程可知,首先确定
,由(2)的求解过程可知,首先确定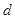 的范围,即
的范围,即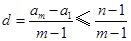 ,由于
,由于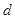 只能取正整数,故取
只能取正整数,故取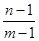 的整数部分是
的整数部分是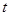 ,即
,即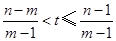 ,
,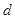 的可能取值为
的可能取值为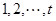 ,计算出
,计算出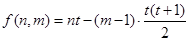 ,利用
,利用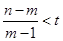 即可证得结论.
即可证得结论.试题解析:(1)符合要求的递增等差数列为1,2,3;2,3,4;3,4,5;1,3,5,共4个.
所以
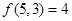 . 3分
. 3分(2)设满足条件的一个等差数列首项为
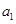 ,公差为
,公差为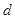 ,
,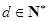 .
.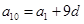 ,
,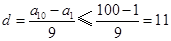 ,
,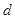 的可能取值为
的可能取值为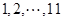 .
.对于给定的
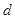 ,
,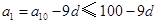 , 当
, 当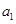 分别取
分别取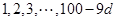 时,可得递增等差数列
时,可得递增等差数列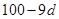 个(如:
个(如: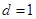 时,
时,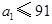 ,当
,当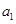 分别取
分别取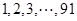 时,可得递增等差数列91个:
时,可得递增等差数列91个: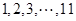 ;
;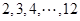 ;
;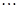 ;
;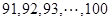 ,其它同理).
,其它同理).所以当
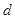 取
取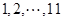 时,可得符合要求的等差数列的个数为:
时,可得符合要求的等差数列的个数为: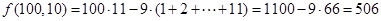 . 8分
. 8分(3)设等差数列首项为
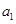 ,公差为
,公差为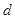 ,
,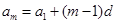 ,
,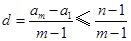 ,
,记
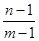 的整数部分是
的整数部分是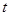 ,则
,则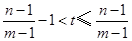 ,即
,即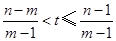 .
.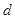 的可能取值为
的可能取值为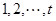 ,
,对于给定的
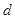 ,
,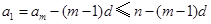 ,当
,当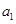 分别取
分别取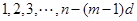 时,可得递增等差数列
时,可得递增等差数列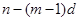 个.
个.所以当
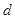 取
取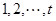 时,得符合要求的等差数列的个数
时,得符合要求的等差数列的个数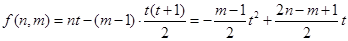
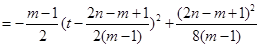
易证
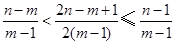 .
.又因为
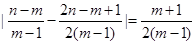 ,
,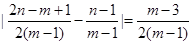 ,
,所以
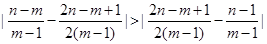 .
.所以
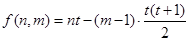
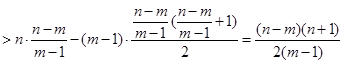 .
.即
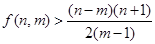 . 13分
. 13分
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 }的前n项和为Sn,且S4=4S2,
}的前n项和为Sn,且S4=4S2, .
. }满足
}满足 ,求{
,求{ 恒成立.若有,求出K的最大值,若没有,说明理由.
恒成立.若有,求出K的最大值,若没有,说明理由. 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
. ,且该数列前
,且该数列前 最大,求
最大,求 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值; ,则数列
,则数列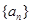 中,如果
中,如果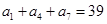 ,
,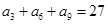 ,则数列
,则数列 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )
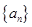 中,已知
中,已知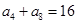 ,则该数列前11项和
,则该数列前11项和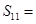 ( )
( )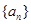 ,
,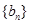 满足:
满足: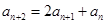 ,
,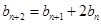 ,
,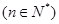 ,那么( )
,那么( )


 是等差数列
是等差数列 的前
的前 项和,
项和, ,则
,则 的值为( )
的值为( )



 中,
中, ,
, ,
, ,则
,则
 = .
= .