题目内容
二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V= πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度
πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度 ▲ .
▲ .
 πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度
πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度 ▲ .
▲ .
解:因为利用类比推理,将平面的转化为空间问题,二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V= πr3;四维空间中“超球”的三维测度V=8πr3,那么四维测度
πr3;四维空间中“超球”的三维测度V=8πr3,那么四维测度
 ,系数由二维中除以2,三维中除以3,思维中除以4,次数上几维就是几次幂,因此为答案
,系数由二维中除以2,三维中除以3,思维中除以4,次数上几维就是几次幂,因此为答案
 πr3;四维空间中“超球”的三维测度V=8πr3,那么四维测度
πr3;四维空间中“超球”的三维测度V=8πr3,那么四维测度
 ,系数由二维中除以2,三维中除以3,思维中除以4,次数上几维就是几次幂,因此为答案
,系数由二维中除以2,三维中除以3,思维中除以4,次数上几维就是几次幂,因此为答案

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 ;
; 的体积;
的体积; 

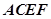 所在平面与矩形
所在平面与矩形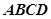 所在平面垂直,
所在平面垂直,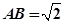 ,
,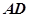 =1,
=1,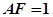 ,
,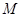 是线段
是线段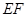 的中点.
的中点.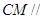 平面
平面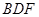 ;
;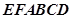 的表面积;
的表面积;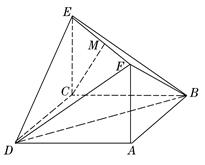
 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边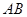 、
、 上,且
上,且 ,
, ,将此正方形沿
,将此正方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥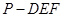 的体积是
的体积是










 ,其余棱长都为1,其体积为
,其余棱长都为1,其体积为 ,则函数
,则函数