题目内容
18.若正数x,y满足$\frac{2}{x}$+$\frac{3}{y}$=2,则xy的最小值是6.分析 利用基本不等式的性质即可得出.
解答 解:∵正数x,y满足$\frac{2}{x}$+$\frac{3}{y}$=2,
∴$2≥2\sqrt{\frac{2}{x}•\frac{3}{y}}$,化为xy≥6,当且仅当$\frac{2}{x}=\frac{3}{y}$=1时取等号.
则xy的最小值是6.
故答案为:6.
点评 本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=( )
| A. | [1,3) | B. | (1,3) | C. | [0,2] | D. | (1,4) |
10.若sin2xsin3x=cos2xcos3x,则x的值是( )
| A. | $\frac{π}{10}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{4}$ |
8.一个学生通过某种英语听力测试的概率是$\frac{1}{2}$,他连续测试2次,那么其中恰有1次获得通过的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
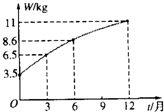 有下列四个结论,
有下列四个结论,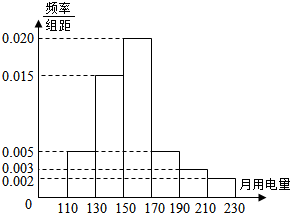 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示,则该小区居民用电量的中位数为155,平均数为156.8.
某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示,则该小区居民用电量的中位数为155,平均数为156.8.