题目内容
以椭圆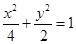 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
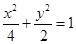 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )A.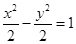 | B. | C. | D. |
A
试题分析:由椭圆方程可知所求双曲线的焦点为
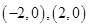 ,顶点为
,顶点为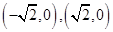 。则设双曲线方程为
。则设双曲线方程为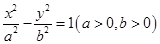 ,所以
,所以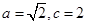 ,则
,则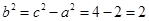 。所以所求双曲线方程为
。所以所求双曲线方程为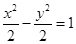 。故A正确。
。故A正确。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
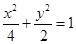 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )A.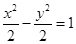 | B. | C. | D. |
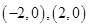 ,顶点为
,顶点为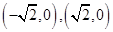 。则设双曲线方程为
。则设双曲线方程为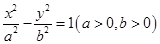 ,所以
,所以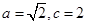 ,则
,则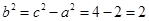 。所以所求双曲线方程为
。所以所求双曲线方程为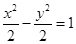 。故A正确。
。故A正确。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案