题目内容
已知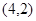 是直线
是直线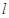 被椭圆
被椭圆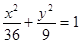 所截得的线段的中点,则直线
所截得的线段的中点,则直线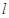 的方程是( )
的方程是( )
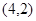 是直线
是直线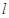 被椭圆
被椭圆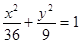 所截得的线段的中点,则直线
所截得的线段的中点,则直线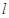 的方程是( )
的方程是( )A. | B. |
C. | D. |
D
试题分析:利用“点差法”即可得出直线
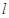 的斜率,即设直线
的斜率,即设直线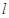 与椭圆相交于两点
与椭圆相交于两点 ,代入椭圆方程得
,代入椭圆方程得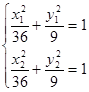 ,两式相减得
,两式相减得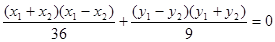 ,由
,由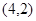 为
为 两点的中点可知
两点的中点可知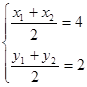 代入上式可求直线
代入上式可求直线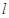 的斜率,然后利用点斜式即可得出方程.
的斜率,然后利用点斜式即可得出方程.
练习册系列答案
相关题目
题目内容
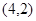 是直线
是直线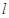 被椭圆
被椭圆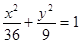 所截得的线段的中点,则直线
所截得的线段的中点,则直线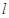 的方程是( )
的方程是( )A. | B. |
C. | D. |
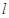 的斜率,即设直线
的斜率,即设直线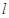 与椭圆相交于两点
与椭圆相交于两点 ,代入椭圆方程得
,代入椭圆方程得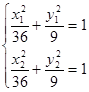 ,两式相减得
,两式相减得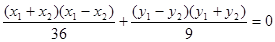 ,由
,由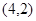 为
为 两点的中点可知
两点的中点可知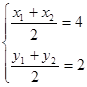 代入上式可求直线
代入上式可求直线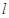 的斜率,然后利用点斜式即可得出方程.
的斜率,然后利用点斜式即可得出方程.