题目内容
已知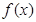 为偶函数,且
为偶函数,且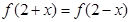 ,当
,当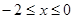 时,
时,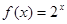 ,若
,若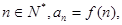 则
则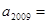
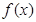 为偶函数,且
为偶函数,且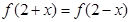 ,当
,当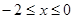 时,
时,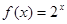 ,若
,若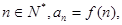 则
则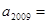
A.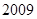 | B.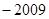 | C.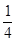 | D.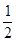 |
D
此题考查偶函数的性质
解:由于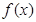 为偶函数,所以
为偶函数,所以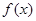 的图象关于
的图象关于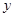 轴对称,又
轴对称,又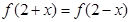 所以
所以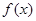 的图象关于
的图象关于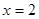 对称,故函数的周期为2,所以
对称,故函数的周期为2,所以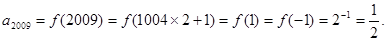
答案:D.
解:由于
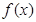 为偶函数,所以
为偶函数,所以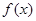 的图象关于
的图象关于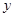 轴对称,又
轴对称,又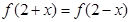 所以
所以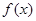 的图象关于
的图象关于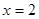 对称,故函数的周期为2,所以
对称,故函数的周期为2,所以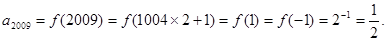
答案:D.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
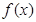 为偶函数,且
为偶函数,且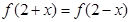 ,当
,当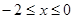 时,
时,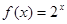 ,若
,若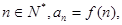 则
则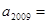
A.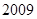 | B.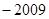 | C.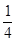 | D.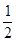 |
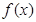 为偶函数,所以
为偶函数,所以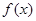 的图象关于
的图象关于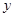 轴对称,又
轴对称,又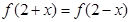 所以
所以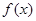 的图象关于
的图象关于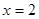 对称,故函数的周期为2,所以
对称,故函数的周期为2,所以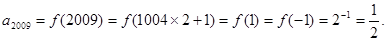

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案