题目内容
已知数列{an}的通项公式为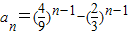 ,则数列{an}( )
,则数列{an}( )A.有最大项,没有最小项
B.有最小项,没有最大项
C.既有最大项又有最小项
D.既没有最大项也没有最小项
【答案】分析:把数列的通项公式看作函数解析式,令 ,换元后是二次函数解析式,内层是指数函数,由指数函数的性质可以求出t的大致范围,在求出的范围内分析二次函数的最值情况.
,换元后是二次函数解析式,内层是指数函数,由指数函数的性质可以求出t的大致范围,在求出的范围内分析二次函数的最值情况.
解答:解: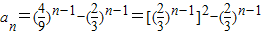
令 ,则t是区间(0,1]内的值,而
,则t是区间(0,1]内的值,而 =
= ,
,
所以当n=1,即t=1时,an取最大值,使 最接近
最接近 的n的值为数列{an}中的最小项,
的n的值为数列{an}中的最小项,
所以该数列既有最大项又有最小项.
故选C.
点评:本题考查了数列的函数特性,考查了换元法,解答此题的关键是由外层二次函数的最值情况断定n的取值,从而说明使数列取得最大项和最小项的n都存在,属易错题.
 ,换元后是二次函数解析式,内层是指数函数,由指数函数的性质可以求出t的大致范围,在求出的范围内分析二次函数的最值情况.
,换元后是二次函数解析式,内层是指数函数,由指数函数的性质可以求出t的大致范围,在求出的范围内分析二次函数的最值情况.解答:解:
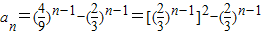
令
 ,则t是区间(0,1]内的值,而
,则t是区间(0,1]内的值,而 =
= ,
,所以当n=1,即t=1时,an取最大值,使
 最接近
最接近 的n的值为数列{an}中的最小项,
的n的值为数列{an}中的最小项,所以该数列既有最大项又有最小项.
故选C.
点评:本题考查了数列的函数特性,考查了换元法,解答此题的关键是由外层二次函数的最值情况断定n的取值,从而说明使数列取得最大项和最小项的n都存在,属易错题.

练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|