题目内容
6. 如图,在四棱锥P-ABCD中底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,作EF⊥PB于点F.
如图,在四棱锥P-ABCD中底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,作EF⊥PB于点F.(1)证明PB⊥平面EFD;
(2)求PA与平面PDB所成角的正弦值.
分析 (1)利用线面垂直的判定与性质定理可得DE⊥PB,又EF⊥PB,即可证明.
(2)连接AC交PD于O,连接OP,由于AO⊥平面PBD,可得∠OPA即为PA与平面PDB所成角.利用直角三角形的边角关系即可得出.
解答 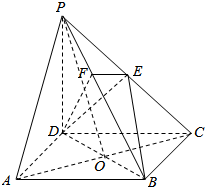 (1)证明:∵PD⊥面ABCD,∴PD⊥BC,
(1)证明:∵PD⊥面ABCD,∴PD⊥BC,
又BC⊥DC,
∴BC⊥面PDC,
∴DE⊥BC
又DE⊥PC,
∴DE⊥面PBC,
∴DE⊥PB,
又已知EF⊥PB,
∴PB⊥面DEF.
(2)解:连接AC交PD于O,连接OP,
∵AO⊥平面PBD,
∴∠OPA即为PA与平面PDB所成角.
在Rt△PAD中,PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{2}$AD,
在Rt△AOP中,sin∠OPA=$\frac{OA}{PA}$=$\frac{{\frac{{\sqrt{2}}}{2}AD}}{{\sqrt{2}AD}}$=$\frac{1}{2}$.
∴sin∠OPA=$\frac{1}{2}$.
点评 本题考查了线面垂直的判定与性质定理、线面角、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目