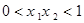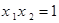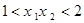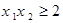题目内容
定义在R上的单调函数f(x),存在实数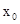 ,使得对于任意
,使得对于任意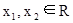 ,
,
都有: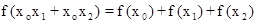 恒成立.
恒成立.
(Ⅰ)求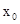 的值;
的值;
(Ⅱ)若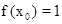 ,且对任意正整数n,有
,且对任意正整数n,有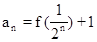 ,又数列
,又数列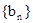 满足
满足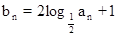 ,求
,求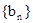 的通项公式.
的通项公式.
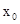 ,使得对于任意
,使得对于任意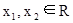 ,
,都有:
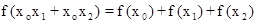 恒成立.
恒成立.(Ⅰ)求
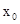 的值;
的值;(Ⅱ)若
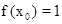 ,且对任意正整数n,有
,且对任意正整数n,有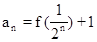 ,又数列
,又数列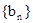 满足
满足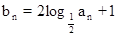 ,求
,求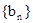 的通项公式.
的通项公式.(Ⅰ)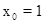 (Ⅱ)
(Ⅱ)
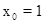 (Ⅱ)
(Ⅱ)
本试题主要是考查了函数的赋值思想的运用iji求解哈数的递归关系式运用。
(1)令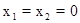 得
得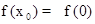
令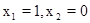 得
得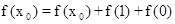 即f(1)=-f(0)
即f(1)=-f(0)
∴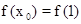 又f(x)在R上单调,∴
又f(x)在R上单调,∴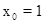
(2)由(1)得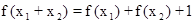
∴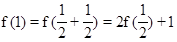
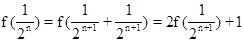 ,然后得到分析证明。
,然后得到分析证明。
解:(1)令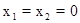 得
得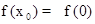 ………(2分)
………(2分)
令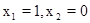 得
得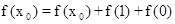 即f(1)=-f(0)
即f(1)=-f(0)
∴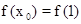 又f(x)在R上单调,∴
又f(x)在R上单调,∴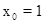 …………………(5分)
…………………(5分)
(2)由(1)得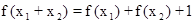
∴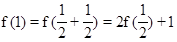 ……………………(6分)
……………………(6分)
∴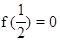 ∴
∴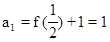
∴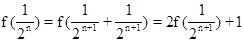 …………………………(9分)
…………………………(9分)
∴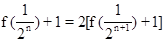 即
即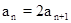 ∴
∴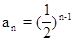
∴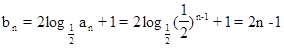 …………………(12分)
…………………(12分)
(1)令
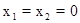 得
得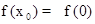
令
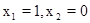 得
得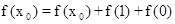 即f(1)=-f(0)
即f(1)=-f(0)∴
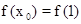 又f(x)在R上单调,∴
又f(x)在R上单调,∴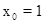
(2)由(1)得
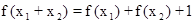
∴
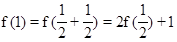
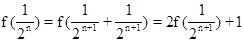 ,然后得到分析证明。
,然后得到分析证明。解:(1)令
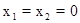 得
得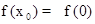 ………(2分)
………(2分)令
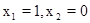 得
得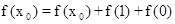 即f(1)=-f(0)
即f(1)=-f(0)∴
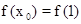 又f(x)在R上单调,∴
又f(x)在R上单调,∴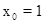 …………………(5分)
…………………(5分)(2)由(1)得
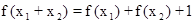
∴
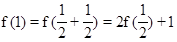 ……………………(6分)
……………………(6分)∴
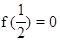 ∴
∴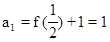
∴
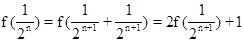 …………………………(9分)
…………………………(9分)∴
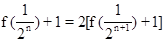 即
即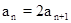 ∴
∴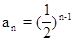
∴
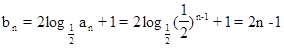 …………………(12分)
…………………(12分) 
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
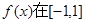 上是单调函数,且
上是单调函数,且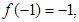 若函数
若函数 对所有的
对所有的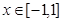 都成立,当
都成立,当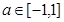 时,则
时,则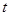 的取值范围是
的取值范围是 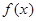 在(0,+∞)上是增函数,(
在(0,+∞)上是增函数,( ,0)上也是增函数,所以
,0)上也是增函数,所以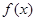 是增函数;
是增函数;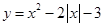 的递增区间为
的递增区间为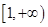 ;
;  则
则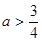 ;
;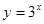 的图象与函数y=log3x的图象关于直线y=x对称;
的图象与函数y=log3x的图象关于直线y=x对称;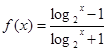 ,若
,若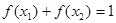 (其中
(其中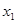 、
、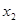 均大于2),则
均大于2),则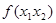 的最小值为 。
的最小值为 。 (其中
(其中 )在区间
)在区间 上单调递减,则实数
上单调递减,则实数 的取值范围为 。
的取值范围为 。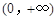 上的函数
上的函数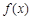 满足:对任意
满足:对任意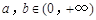 ,都有
,都有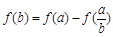 ,且当
,且当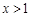 时,
时,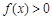 .
.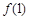 的值;
的值; ,解不等式
,解不等式 .
. ,定义
,定义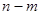 为区间
为区间 在任意长度为2的闭区间上总存在两点
在任意长度为2的闭区间上总存在两点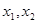 ,使
,使 成立,则实数
成立,则实数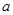 的最小值为
的最小值为  (a为常数)在x=
(a为常数)在x= 处取得极值,则a的
处取得极值,则a的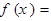
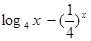 、
、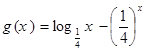 的零点分别为
的零点分别为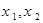 ,则( )
,则( )