题目内容
.对于 ,定义
,定义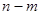 为区间
为区间 的长度,若函数
的长度,若函数 在任意长度为2的闭区间上总存在两点
在任意长度为2的闭区间上总存在两点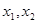 ,使
,使 成立,则实数
成立,则实数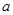 的最小值为
的最小值为
 ,定义
,定义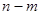 为区间
为区间 的长度,若函数
的长度,若函数 在任意长度为2的闭区间上总存在两点
在任意长度为2的闭区间上总存在两点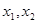 ,使
,使 成立,则实数
成立,则实数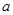 的最小值为
的最小值为 1
要使函数f(x)=ax2-2x+1(a>0)在任意长度为2的闭区间上总存在两点x1,x2,使|f(x1)-f(x2)|≥1成立,只需要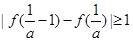 恒成立,
恒成立,
∵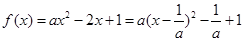 ,∴
,∴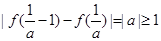
∵a>0,∴a≥1,∴实数a的最小值为1.
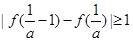 恒成立,
恒成立,∵
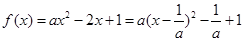 ,∴
,∴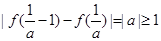
∵a>0,∴a≥1,∴实数a的最小值为1.

练习册系列答案
相关题目
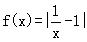
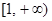 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;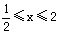 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;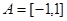 ,
,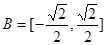 ,函数
,函数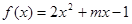 ,
,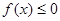 的解集为C,当
的解集为C,当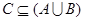 时,求实数
时,求实数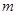 取值范围;
取值范围;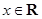 ,都有
,都有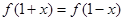 成立,求
成立,求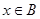 时,
时,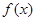 的值域;
的值域;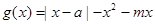
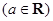 ,求
,求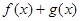 的最小值.
的最小值.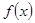 在
在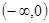 上单调递减,且
上单调递减,且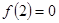 ,则不等式
,则不等式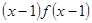 >0的解集是( )
>0的解集是( )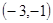
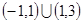
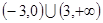
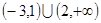
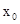 ,使得对于任意
,使得对于任意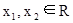 ,
,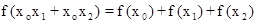 恒成立.
恒成立.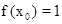 ,且对任意正整数n,有
,且对任意正整数n,有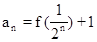 ,又数列
,又数列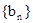 满足
满足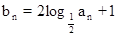 ,求
,求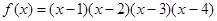 ,则
,则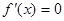 有( )
有( )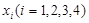
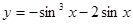 的最小值是__________。
的最小值是__________。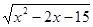 的单调递减区间是 .
的单调递减区间是 .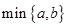 表示
表示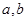 两数中的最小值,若函数
两数中的最小值,若函数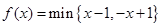 ,则不等式
,则不等式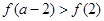 的解集是________________.
的解集是________________.