Question

6．在△ABC中，三个内角A，B，C的对边分别为a，b，c，满足sinA+sinB=sinC（cosB+cosA）．
（1）证明：△ABC是直角三角形；
（2）如图所示，设圆O过A，B，C三点，c=2，∠BAC=$\frac{π}{6}$，点P位于劣弧$\widehat{AC}$上，求△PAC面积的最大值．

Answer 1

分析 （1）由已知利用正弦定理和余弦定理得$\frac{a}{2R}+\frac{b}{2R}$=$\frac{c}{2R}$（$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$），由此利用勾股定理能证明△ABC是直角三角形．
（2）由已知得∠C=90°，当OP⊥AC时，△PAC面积最大，由此能求出△PAC面积的最大值．

解答 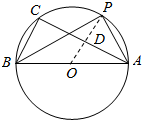（1）证明：∵在△ABC中，三个内角A，B，C的对边分别为a，b，c，满足sinA+sinB=sinC（cosB+cosA），
∴$\frac{a}{2R}+\frac{b}{2R}$=$\frac{c}{2R}$（$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$），
∴2ab（a+b）=b（a²+c²-b²）+a（b²+c²-a²），
整理，得a²（a+b）+b²（a+b）=c²（a+b），
∴a²+b²=c²，
∴△ABC是直角三角形．
（2）解：由（1）得∠C=90°，∴直径AB=c=2，
∵∠BAC=$\frac{π}{6}$，∴BC=1，AC=$\sqrt{3}$，
∵点P位于劣弧$\widehat{AC}$上，∴当OP⊥AC时，△PAC面积最大，
设OP交AC于D，此时OP=1，AD=CD=$\frac{\sqrt{3}}{2}$，OD=$\sqrt{1-（\frac{\sqrt{3}}{2}）^{2}}$=$\frac{1}{2}$，∴PD=$\frac{1}{2}$，
∴S_△PAC=$\frac{1}{2}×AC×PD$=$\frac{1}{2}×\sqrt{3}×\frac{1}{2}$=$\frac{\sqrt{3}}{4}$．
∴△PAC面积的最大值为$\frac{\sqrt{3}}{4}$．

点评 本题考查直角三角形的证明，考查三角形面积最大值的求法，是中档题，解题时要注意正弦定理、余弦定理、勾股定理、垂径定理的灵活运用．